Unveiling the Power of the 4-Input Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Related Articles: Unveiling the Power of the 4-Input Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of the 4-Input Karnaugh Map: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of the 4-Input Karnaugh Map: A Comprehensive Guide to Boolean Simplification

The realm of digital circuit design often involves the intricate manipulation of Boolean expressions. These expressions, built upon logical operators like AND, OR, and NOT, represent the behavior of digital circuits. However, as circuit complexity grows, simplifying these expressions becomes crucial for efficient hardware implementation. This is where the Karnaugh map, a visual tool for Boolean simplification, emerges as an invaluable asset.

This guide delves into the workings of the 4-input Karnaugh map, providing a comprehensive understanding of its structure, usage, and advantages in simplifying Boolean expressions.

Understanding the Structure of a 4-Input Karnaugh Map

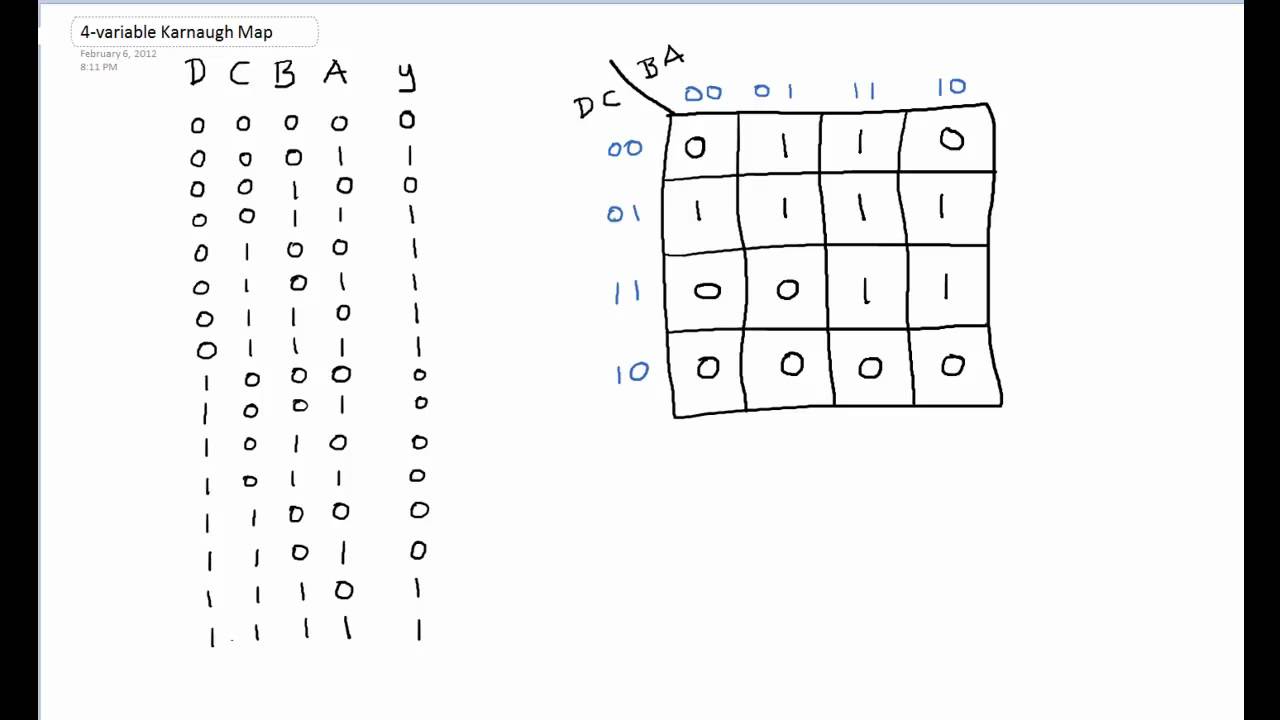
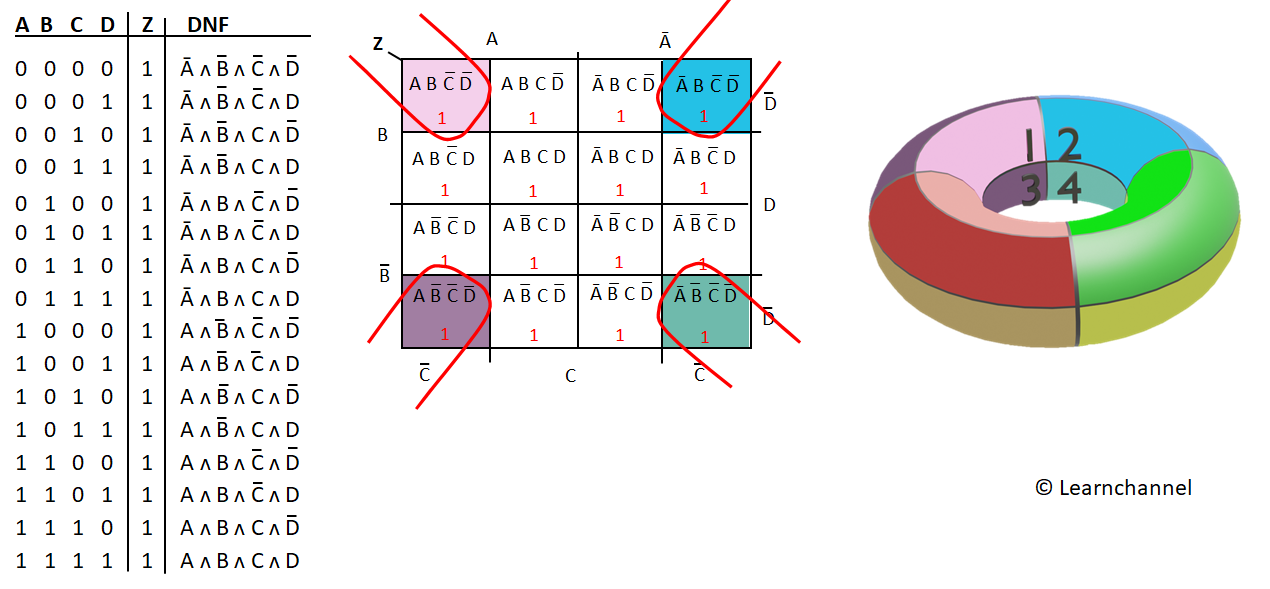
A Karnaugh map is a graphical representation of a truth table, designed to facilitate the identification of minimal Boolean expressions. The map’s structure is based on a grid arrangement, with each cell representing a unique combination of input variables. For a 4-input Karnaugh map, the grid consists of 16 cells, arranged in a 2×4 configuration.

The arrangement of cells is not arbitrary; it follows a specific pattern that ensures adjacent cells differ in only one input variable. This adjacency principle is crucial for grouping adjacent cells containing ‘1’s, a step that leads to simplification.

The following elements define the structure of a 4-input Karnaugh map:

• Rows and Columns: The rows and columns of the map are labeled with binary codes representing the input variables. For a 4-input map, two variables are assigned to rows and the remaining two to columns.
• Gray Code Labeling: The binary codes used for labeling follow the Gray code sequence, ensuring that adjacent cells differ in only one bit. This property is critical for identifying groups of adjacent ‘1’s.
• Cell Representation: Each cell in the map corresponds to a unique combination of input variables. The value within each cell represents the output of the Boolean expression for that specific input combination. A ‘1’ indicates a "true" output, while a ‘0’ represents a "false" output.

The Power of Grouping: Simplifying Boolean Expressions

The core advantage of the Karnaugh map lies in its ability to simplify Boolean expressions by visually identifying groups of adjacent ‘1’s. These groups represent logical terms that can be combined to create a more concise expression.

Here’s how grouping works:

• Adjacent Cells: Cells are considered adjacent if they share a common side (not just a corner). The adjacency principle, based on Gray code labeling, ensures that adjacent cells differ in only one input variable.
• Group Formation: Adjacent cells containing ‘1’s can be grouped together. The larger the group, the more simplification is achieved.
• Minimal Groups: The goal is to cover all ‘1’s in the map using the smallest possible number of groups. This minimizes the number of terms in the simplified expression.
• Group Size: Groups can be of size 1, 2, 4, 8, or 16. The size of a group determines the number of variables involved in the corresponding term. A group of size 2 eliminates one variable, a group of size 4 eliminates two variables, and so on.

A Step-by-Step Guide to Using a 4-Input Karnaugh Map

1. Construct the Map:

• Identify the four input variables and assign them to the rows and columns using Gray code labeling.
• Populate the map with the output values from the truth table.

2. Identify Groups of ‘1’s:

• Start by finding the largest possible groups of adjacent ‘1’s.
• Ensure that all ‘1’s are covered by at least one group.
• Avoid overlapping groups, as this can lead to redundancy.

3. Formulate the Boolean Expression:

• For each group, write a term that represents the common input variables for that group.
• For a group of size 2, the term includes the variable that changes between the two cells.
• For a group of size 4, the term includes the two variables that change between the four cells.
• The final Boolean expression is the sum of the terms corresponding to each group.

4. Minimize the Expression:

• Once the initial expression is formed, look for opportunities to further simplify it.
• This may involve combining terms or eliminating redundant variables.

Illustrative Example: Simplifying a 4-Input Boolean Expression

Let’s consider the following Boolean expression:

F(A, B, C, D) = Σm(0, 1, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15)

1. Construct the Karnaugh Map:

• Assign input variables A and B to the rows and C and D to the columns.
• Populate the map with ‘1’s in the cells corresponding to the minterms listed in the expression.

2. Identify Groups of ‘1’s:

• There are several groups of ‘1’s in the map. The largest group is a group of 8, covering the top row and the bottom row.
• There are also two groups of size 2, each covering a pair of adjacent ‘1’s.

3. Formulate the Boolean Expression:

• The group of size 8 represents the term ‘A’.
• Each group of size 2 represents a term that includes the variable that changes between the two cells.
• The final simplified expression is: F(A, B, C, D) = A + C’D + CD’

4. Minimize the Expression:

• This expression is already in its simplest form.

Benefits of Using a Karnaugh Map

• Simplified Boolean Expressions: Karnaugh maps provide a visual method for identifying minimal Boolean expressions, leading to more efficient hardware implementation.
• Reduced Gate Count: Minimized expressions translate to a reduced number of logic gates required to implement the circuit, saving on hardware resources and reducing power consumption.
• Improved Circuit Performance: Simplified circuits generally exhibit faster switching speeds and lower propagation delays, contributing to improved circuit performance.
• Enhanced Circuit Design: Karnaugh maps aid in the design of more optimized and cost-effective digital circuits.

FAQs about 4-Input Karnaugh Map Calculators

Q: What is a 4-Input Karnaugh Map Calculator?

A: A 4-input Karnaugh map calculator is a software tool that automates the process of simplifying Boolean expressions using a Karnaugh map. It allows users to input the truth table or the Boolean expression and provides the simplified expression as output.

Q: What are the advantages of using a 4-input Karnaugh map calculator?

A: Karnaugh map calculators offer several benefits:

• Time Efficiency: They eliminate the manual effort involved in constructing and analyzing the Karnaugh map, saving time and effort.
• Accuracy: Calculators reduce the risk of errors associated with manual calculations and grouping.
• Accessibility: They provide a convenient and readily available tool for Boolean simplification, especially for students and engineers who may not be familiar with the manual process.

Q: Are there any limitations to using a 4-input Karnaugh map calculator?

A: While Karnaugh map calculators are valuable tools, they have some limitations:

• Complexity: For expressions with more than four input variables, the complexity of the map increases significantly, making manual analysis challenging.
• Limited Functionality: Some calculators may not offer advanced features like handling don’t care conditions or providing multiple solutions.
• Understanding the Process: Overreliance on calculators can hinder the development of a deep understanding of the underlying principles of Boolean simplification.

Tips for Using a 4-Input Karnaugh Map Calculator

• Understand the Basics: Before relying solely on a calculator, gain a solid understanding of the fundamentals of Karnaugh maps and Boolean simplification.
• Choose the Right Calculator: Select a calculator that meets your specific needs and offers features like handling don’t care conditions and providing multiple solutions.
• Verify Results: Always manually verify the results obtained from the calculator to ensure accuracy.
• Explore Alternative Tools: Investigate other Boolean simplification techniques, such as Quine-McCluskey method, for handling more complex expressions.

Conclusion

The 4-input Karnaugh map, with its visual and intuitive approach, empowers digital circuit designers to simplify complex Boolean expressions effectively. While Karnaugh map calculators offer a convenient alternative, a thorough understanding of the underlying principles remains essential for informed design decisions. By mastering the art of using Karnaugh maps, engineers can create efficient, cost-effective, and high-performing digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of the 4-Input Karnaugh Map: A Comprehensive Guide to Boolean Simplification. We appreciate your attention to our article. See you in our next article!