Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Expression Simplification

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Expression Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Expression Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Expression Simplification

The realm of digital logic design hinges on the ability to manipulate and optimize Boolean expressions, the mathematical framework underpinning digital circuits. While traditional algebraic methods can prove cumbersome, Karnaugh maps (K-maps) emerge as a visual and intuitive tool for simplifying these expressions, leading to more efficient and cost-effective circuits. This article delves into the intricacies of K-maps, exploring their construction, utilization, and the remarkable benefits they offer in simplifying Boolean functions.

Understanding the Foundation: Boolean Algebra and Logic Gates

Before embarking on the journey of K-maps, it is essential to grasp the fundamentals of Boolean algebra and logic gates. Boolean algebra, named after George Boole, is a system of mathematics that deals with binary values, typically represented as 0 and 1, representing "false" and "true" respectively. Logic gates, the building blocks of digital circuits, implement these Boolean operations, transforming input signals into output signals based on specific logical rules.

Common logic gates include:

• AND gate: Outputs 1 only when all inputs are 1.
• OR gate: Outputs 1 if at least one input is 1.
• NOT gate: Inverts the input signal.
• XOR gate: Outputs 1 if the inputs are different.
• NAND gate: Outputs 0 only when all inputs are 1.
• NOR gate: Outputs 0 if at least one input is 1.

These gates form the basis for constructing complex digital circuits, and their behavior can be represented using Boolean expressions.

The Essence of Karnaugh Maps: Visualizing Boolean Expressions

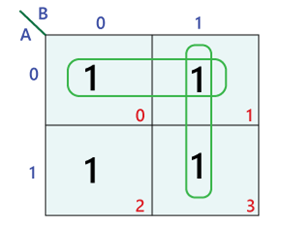
A Karnaugh map, named after Maurice Karnaugh, is a graphical representation of a Boolean function. It provides a systematic method for simplifying Boolean expressions by identifying and grouping adjacent minterms (product terms) that correspond to "1" outputs in the truth table of the function.

Constructing a K-Map: A Step-by-Step Guide

1. Determine the Number of Variables: The number of variables in the Boolean function dictates the size of the K-map. A function with ‘n’ variables requires a 2^n cell K-map. For instance, a 3-variable function necessitates an 8-cell K-map (2^3 = 8).

2. Assign Binary Codes to Cells: Each cell in the K-map represents a unique combination of input variables. The cells are arranged in a specific order, with adjacent cells differing by only one variable. This arrangement is crucial for identifying adjacent minterms.

3. Populate the K-Map: The truth table of the Boolean function is used to populate the K-map. Each cell is assigned a "1" or "0" based on the output of the function for the corresponding input combination.

Simplifying Boolean Expressions with K-Maps: A Practical Approach

Once the K-map is constructed, the simplification process begins by identifying groups of adjacent cells containing "1"s. These groups must adhere to the following rules:

• Adjacent Cells: Cells are considered adjacent if they share a common side, even if they are on opposite ends of the map.
• Groups of Two, Four, Eight, etc.: Groups should contain 2^n cells, where ‘n’ is an integer.
• Largest Possible Groups: Prioritize forming the largest possible groups to achieve maximum simplification.
• Overlapping Groups: Groups can overlap, and cells can belong to multiple groups.

Interpreting the Simplified Expression:

After identifying the groups, each group corresponds to a simplified product term (minterm) in the Boolean expression. The simplified expression is obtained by combining these minterms using the OR operation.

Illustrative Example: Simplifying a 3-Variable Boolean Function

Let’s consider the Boolean function F(A, B, C) = Σ(0, 1, 2, 3, 5, 7).

1. Construct the K-Map: A 3-variable K-map has 8 cells, arranged as follows:

     AB | 00 | 01 | 11 | 10
   C     |     |     |     |
   0     |  1  |  1  |  1  |  1
   1     |  1  |  0  |  1  |  0 

2. Identify Groups: Two groups are identified:

   • Group 1: Cells (0, 1, 2, 3) representing the minterm A’ (NOT A).
   • Group 2: Cells (0, 1, 4, 5) representing the minterm B’ (NOT B).

3. Simplified Expression: The simplified expression is F(A, B, C) = A’ + B’.

Advantages of Using Karnaugh Maps:

• Visual Intuition: K-maps provide a visual representation of the Boolean function, making it easier to identify patterns and simplify expressions.
• Systematic Approach: The grouping rules ensure a systematic and efficient simplification process.
• Reduced Complexity: K-maps effectively handle complex expressions, simplifying them into more manageable forms.
• Optimized Circuits: Simplified expressions lead to simpler and more efficient digital circuits, reducing component count and power consumption.

FAQs: Addressing Common Questions

Q: Can K-maps be used for functions with more than four variables?

A: While K-maps are most effective for functions with up to four variables, they can be extended to handle more variables using a technique called "map folding". However, the complexity of the map increases significantly with more variables, making the process less intuitive.

Q: What if there are no groups of adjacent "1"s in the K-map?

A: If no groups can be formed, the expression cannot be further simplified using K-maps. In such cases, the original expression remains unchanged.

Q: Can K-maps be used for functions with "don’t care" conditions?

A: Yes, K-maps can accommodate "don’t care" conditions, represented by ‘X’ in the map. These conditions allow for greater flexibility in grouping and can lead to further simplification.

Tips for Efficient K-Map Utilization:

• Start with the Truth Table: Constructing the truth table first provides a clear understanding of the function’s behavior.
• Use a Grid Paper: Using grid paper with squares of appropriate size facilitates accurate and organized K-map construction.
• Highlight Groups: Using different colors or symbols to highlight the groups makes the simplification process more visually appealing and easier to follow.
• Verify the Simplified Expression: After simplification, verify the result by comparing the truth table of the simplified expression with the original truth table.

Conclusion: Empowering Digital Logic Design with K-Maps

Karnaugh maps stand as a powerful tool in the arsenal of digital logic designers. They provide a visually intuitive and systematic method for simplifying Boolean expressions, leading to more efficient and cost-effective circuits. By understanding the principles of K-map construction, grouping rules, and interpretation, designers can unlock the potential for optimizing complex digital systems, paving the way for innovation in the field of digital electronics.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Expression Simplification. We thank you for taking the time to read this article. See you in our next article!