Unveiling the Power of 3-Variable Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Related Articles: Unveiling the Power of 3-Variable Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of 3-Variable Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of 3-Variable Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

The realm of digital logic thrives on the manipulation of binary signals, often represented through Boolean expressions. These expressions, while powerful in describing logic functions, can become complex and unwieldy as the number of variables increases. To tame this complexity and derive efficient logic circuits, engineers rely on a visual tool known as the Karnaugh map. This article delves into the intricacies of 3-variable Karnaugh maps, providing a comprehensive understanding of their construction, usage, and significance in simplifying Boolean expressions.

Understanding the Foundation: Boolean Algebra and Logic Gates

Before embarking on the exploration of Karnaugh maps, a foundational understanding of Boolean algebra and logic gates is crucial. Boolean algebra, named after George Boole, is a system of logic that deals with binary values, typically represented as 0 and 1. These values correspond to "false" and "true" states, respectively. Logic gates, the building blocks of digital circuits, perform specific Boolean operations on these binary inputs.

Common logic gates include:

• AND gate: Outputs a "1" only if all inputs are "1."
• OR gate: Outputs a "1" if at least one input is "1."
• NOT gate: Inverts the input, turning "1" to "0" and vice versa.
• XOR gate: Outputs a "1" if the inputs are different.
• NAND gate: Outputs a "0" only if all inputs are "1."
• NOR gate: Outputs a "0" if at least one input is "1."

Boolean expressions are formed by combining these logic gates and variables. For instance, the expression "A AND B" represents the output of an AND gate with inputs A and B.

Introducing the Karnaugh Map: A Visual Approach to Simplification

The Karnaugh map, invented by Maurice Karnaugh, is a graphical representation of Boolean functions. It provides a visual framework for simplifying Boolean expressions by identifying and grouping adjacent terms that can be combined using Boolean algebra laws.

A 3-variable Karnaugh map is structured as a 2×4 grid, where each cell represents a unique combination of the three input variables. The arrangement of cells follows a specific pattern, ensuring that adjacent cells differ in only one variable. This arrangement is crucial for identifying groups of adjacent terms that can be simplified.

Constructing a 3-Variable Karnaugh Map: A Step-by-Step Guide

The construction of a 3-variable Karnaugh map involves the following steps:

1. Define the Variables: Identify the three input variables for the Boolean function.
2. Label the Rows and Columns: Label the rows and columns of the 2×4 grid with the binary combinations of two of the variables. The order of the labels must follow a Gray code sequence, where only one bit changes between adjacent cells.
3. Assign Values to Cells: For each possible combination of input variables, determine the corresponding output value of the Boolean function. Enter this value (0 or 1) in the corresponding cell of the Karnaugh map.

Utilizing the Karnaugh Map: Unveiling the Power of Simplification

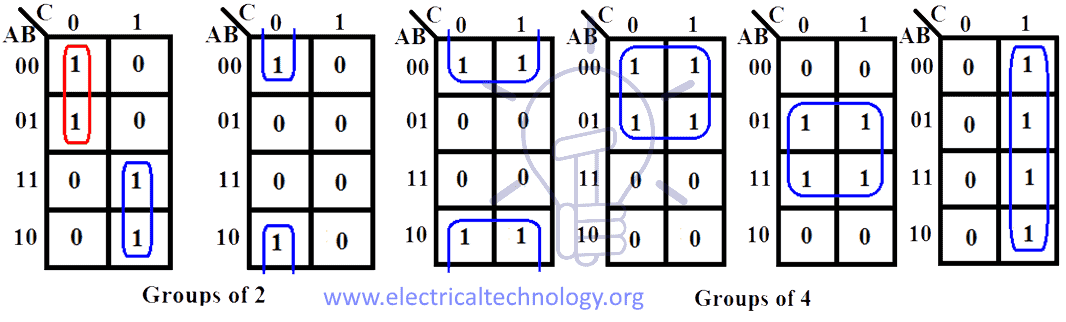
Once the Karnaugh map is constructed, the process of simplifying the Boolean expression begins. This involves identifying groups of adjacent cells containing "1"s. These groups, known as prime implicants, represent terms that can be combined using Boolean algebra laws.

The following rules govern the identification and combination of prime implicants:

1. Group Formation: Prime implicants must consist of adjacent cells, where adjacency is defined as cells sharing a common edge. Cells in the top and bottom rows or left and right columns are also considered adjacent.
2. Group Size: Prime implicants can contain 1, 2, 4, or 8 cells. The larger the group, the simpler the resulting Boolean term.
3. Minimal Coverage: All cells containing "1"s must be covered by at least one prime implicant.

By identifying and combining prime implicants, the Karnaugh map allows for the simplification of the Boolean expression, resulting in a more efficient logic circuit.

Illustrative Example: Simplifying a Boolean Expression with a 3-Variable Karnaugh Map

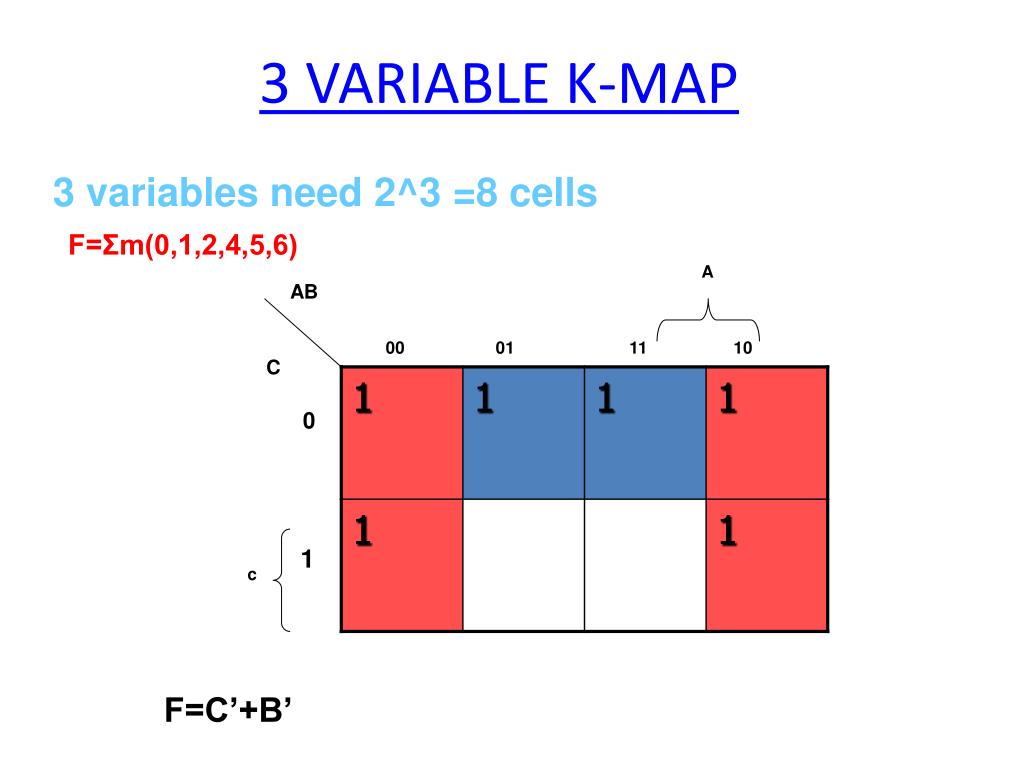
Consider the Boolean expression:

F(A, B, C) = A'B'C' + A'BC' + AB'C' + ABC'

To simplify this expression using a Karnaugh map:

1. Construct the Map: Label the rows with "B" and "C" and the columns with "A," following the Gray code sequence. Enter the output values for each combination of A, B, and C into the corresponding cells.

2. Identify Prime Implicants: Observe that the cells containing "1"s form two groups:

   • Group 1: Cells representing A’B’C’ and A’BC’
   • Group 2: Cells representing AB’C’ and ABC’

3. Combine Prime Implicants: Group 1 represents the term A’C’, and Group 2 represents the term AC’.

4. Simplified Expression: The simplified expression is:

   F(A, B, C) = A'C' + AC'

This simplified expression represents a logic circuit that is more efficient and easier to implement compared to the original expression.

Advantages of Utilizing Karnaugh Maps: A Comprehensive View

The use of Karnaugh maps offers several advantages in simplifying Boolean expressions and designing logic circuits:

• Visual Simplification: The graphical representation of the Karnaugh map provides a clear and intuitive way to identify and combine terms, making the simplification process more straightforward.
• Minimization of Logic Gates: By simplifying the Boolean expression, the Karnaugh map reduces the number of logic gates required to implement the function, leading to a more efficient and compact circuit.
• Enhanced Circuit Performance: Minimizing the number of logic gates reduces the propagation delay and power consumption of the circuit, improving its overall performance.
• Error Reduction: The visual nature of the Karnaugh map helps in identifying and correcting errors that might occur during the simplification process.
• Ease of Implementation: The simplified Boolean expression derived from the Karnaugh map can be easily implemented using standard logic gates, facilitating the design and fabrication of digital circuits.

Addressing Common Concerns: FAQs Regarding 3-Variable Karnaugh Maps

1. Can Karnaugh maps be used for functions with more than three variables?

While Karnaugh maps are effective for functions with up to four variables, their visual representation becomes increasingly complex for functions with more variables. For functions with more than four variables, other simplification techniques like Quine-McCluskey method or Espresso algorithm are typically employed.

2. What happens if there are no adjacent cells containing "1"s?

If no adjacent cells contain "1"s, the Boolean expression cannot be further simplified. Each cell containing a "1" will represent a separate term in the minimized expression.

3. Are there any limitations to using Karnaugh maps?

Karnaugh maps are primarily suited for simplifying Boolean expressions with a small number of variables. Their effectiveness diminishes as the number of variables increases, making other methods more appropriate for complex functions.

4. How can I learn more about Karnaugh maps?

Numerous resources are available online and in textbooks that provide detailed explanations and examples of Karnaugh maps. These resources cover the construction, usage, and application of Karnaugh maps in digital logic design.

Tips for Effective Utilization of 3-Variable Karnaugh Maps: A Guide to Optimization

1. Master the Gray Code: Understanding the Gray code sequence is crucial for correctly labeling the rows and columns of the Karnaugh map. This ensures that adjacent cells differ in only one variable.
2. Identify all Prime Implicants: Thoroughly examine the Karnaugh map to ensure that all prime implicants have been identified. Overlooking prime implicants can lead to a less simplified expression.
3. Consider Don’t Care Conditions: If certain input combinations are not relevant to the function, they can be represented as "don’t care" conditions (represented by "X") on the Karnaugh map. These "don’t care" conditions can be used to form larger prime implicants, leading to further simplification.
4. Use a Systematic Approach: Employ a systematic approach when identifying and combining prime implicants. This helps to ensure that all possibilities are considered and that the resulting expression is truly minimized.

Conclusion: The Enduring Importance of Karnaugh Maps in Digital Logic Design

Karnaugh maps remain a powerful and versatile tool in the field of digital logic design. Their ability to visually simplify Boolean expressions and minimize logic circuits has made them indispensable for engineers and students alike. While other simplification techniques may be more suitable for complex functions with a large number of variables, the simplicity and intuitive nature of Karnaugh maps make them an invaluable asset for understanding and manipulating Boolean logic. By mastering the principles and techniques outlined in this guide, individuals can harness the power of Karnaugh maps to design efficient and robust digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of 3-Variable Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. We hope you find this article informative and beneficial. See you in our next article!