Unraveling Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

Related Articles: Unraveling Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unraveling Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

Unraveling Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

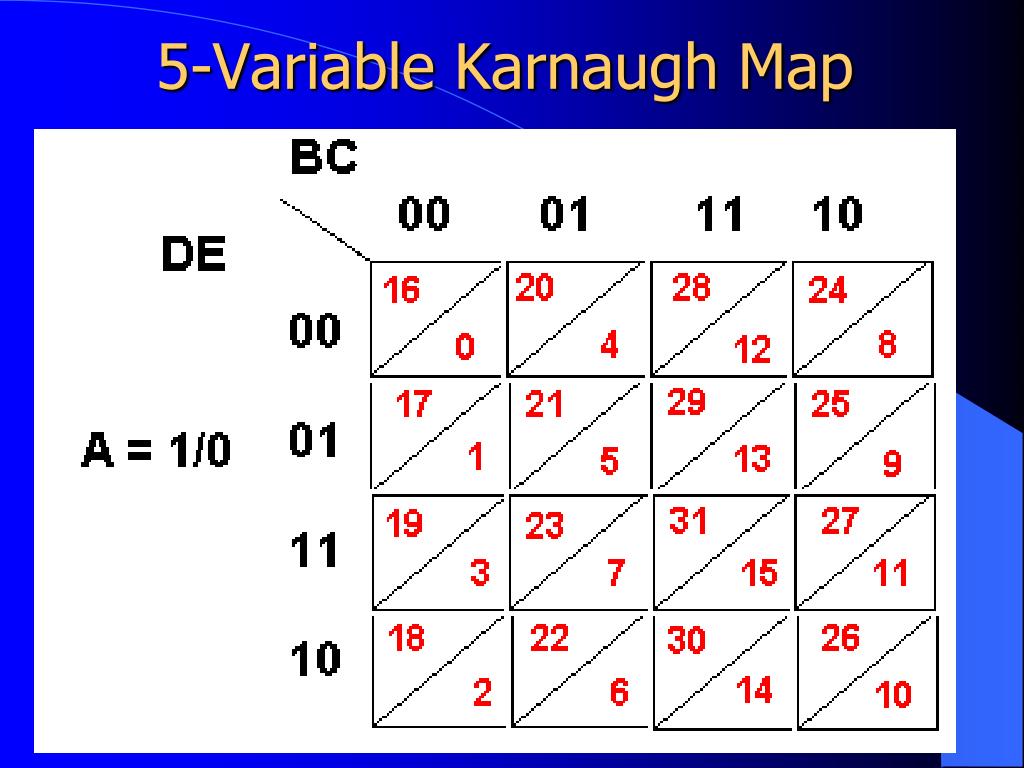
The realm of digital logic design thrives on the ability to efficiently represent and simplify complex Boolean expressions. While truth tables provide a straightforward method, their size grows exponentially with the number of variables, becoming unwieldy for even moderately complex circuits. This is where Karnaugh maps, also known as K-maps, emerge as a powerful tool for simplifying Boolean expressions and optimizing circuit design.

This article delves into the intricacies of 5-variable Karnaugh maps, exploring their construction, application, and the benefits they offer in digital logic design.

Understanding the Foundation: Karnaugh Maps and Their Essence

A Karnaugh map is a graphical representation of a Boolean function, visually organizing the function’s output for all possible combinations of input variables. The map’s structure is based on a grid arrangement, where each cell corresponds to a unique combination of input variables. The key to the map’s effectiveness lies in its ability to exploit the inherent adjacency relationships between cells, allowing for the identification and grouping of adjacent cells representing minterms (product terms) that can be combined to simplify the Boolean expression.

Constructing the 5-Variable Karnaugh Map: A Visual Journey

A 5-variable Karnaugh map is a three-dimensional representation, typically visualized as a series of 2-dimensional maps stacked on top of each other. Each 2-dimensional map represents a particular combination of two variables, while the third dimension is represented by the remaining three variables.

Here’s a step-by-step guide to constructing a 5-variable Karnaugh map:

1. Define the Variables: Identify the five input variables, labeling them with appropriate symbols (e.g., A, B, C, D, E).

2. Create the 2D Maps: Construct four 2-dimensional Karnaugh maps, each representing a different combination of two variables (e.g., AB, AC, AD, AE). Each map will have 16 cells, representing all possible combinations of the two chosen variables.

3. Label the Cells: Label the rows and columns of each map with the binary values of the two chosen variables. It’s crucial to follow a Gray code sequence, ensuring that adjacent cells differ by only one bit, facilitating the identification of adjacent minterms.

4. Stack the Maps: Arrange the four maps vertically, representing the third, fourth, and fifth variables. Each map corresponds to a specific value of the third variable. The fourth and fifth variables are represented by their binary values, changing across the maps in a Gray code sequence.

5. Populate the Cells: For each possible combination of input variables, determine the output of the Boolean function and mark the corresponding cell on the map with a ‘1’ if the output is true and a ‘0’ if the output is false.

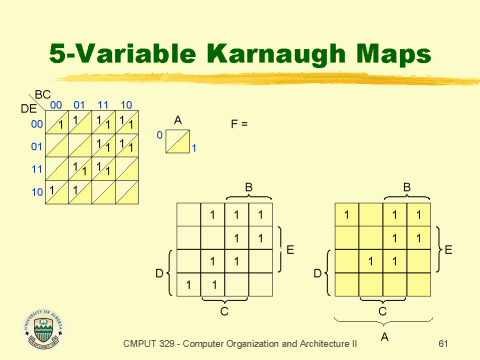
Simplifying Boolean Expressions: The Art of Grouping

The true power of Karnaugh maps lies in their ability to simplify Boolean expressions. This is achieved by identifying and grouping adjacent cells containing ‘1’s. The key principles for grouping are:

1. Adjacency: Cells are considered adjacent if they differ in only one variable, even if they appear on different maps. This includes cells on the edges of the maps, which are considered adjacent to cells on the opposite edge.

2. Group Size: Groups should be as large as possible, ideally powers of two (2, 4, 8, 16). Larger groups represent more simplified terms in the Boolean expression.

3. Rectangle Shape: Groups must be rectangular in shape, with sides aligned with the grid lines.

4. Overlapping: Groups can overlap, allowing for more efficient simplification.

Deriving the Simplified Expression: From Groups to Logic

Once the groups have been identified, the simplified Boolean expression can be derived using the following steps:

1. Identify the Variables: For each group, identify the variables that remain constant within the group. These variables will be included in the product term representing the group.

2. Invert Variables: If a variable is ‘0’ within a group, its complement is included in the product term.

3. Combine Groups: Combine the product terms from each group using the OR operator.

Illustrative Example: A 5-Variable Karnaugh Map in Action

Consider the Boolean function:

F(A, B, C, D, E) = Σm(0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30)

To simplify this function using a 5-variable Karnaugh map:

1. Construct the Map: Create four 2D maps, representing the combinations AB, AC, AD, and AE. Label the rows and columns with Gray code sequences. Stack the maps vertically, representing the variables C, D, and E.

2. Populate the Map: Mark the cells corresponding to the minterms listed in the function’s sum-of-products form (Σm).

3. Identify Groups: Several groups can be formed, including a group of 16 cells covering the entire map, representing the constant term ‘1’.

4. Derive the Expression: The simplified expression is: F(A, B, C, D, E) = 1

This example demonstrates the remarkable simplification achieved using a 5-variable Karnaugh map. The original expression, with 16 minterms, is reduced to a single constant term.

Benefits of Using 5-Variable Karnaugh Maps

The application of 5-variable Karnaugh maps offers several advantages in digital logic design:

1. Simplified Logic: The ability to visually identify and group adjacent minterms significantly simplifies Boolean expressions, leading to more efficient and cost-effective circuit implementations.

2. Reduced Circuit Complexity: Simplified expressions translate to circuits with fewer gates, reducing the overall circuit complexity, power consumption, and cost.

3. Improved Performance: Simpler circuits generally exhibit faster signal propagation times, leading to improved performance and faster processing speeds.

4. Enhanced Readability: The graphical representation of Karnaugh maps provides a clear and intuitive understanding of the Boolean function, enhancing readability and facilitating debugging.

5. Optimized Design: By enabling the identification of redundant terms and minimizing the number of gates, Karnaugh maps contribute to optimized circuit design, maximizing performance and minimizing resource utilization.

FAQs: Addressing Common Concerns

Q: What are the limitations of 5-variable Karnaugh maps?

A: While 5-variable maps are powerful tools, they become cumbersome for functions with more variables. The complexity of visualizing and manipulating the map increases significantly beyond five variables.

Q: Are there alternatives to Karnaugh maps for simplifying Boolean expressions?

A: Yes, several alternatives exist, including:

• Quine-McCluskey Method: A tabular method for simplifying Boolean expressions, suitable for larger numbers of variables.

• Espresso Algorithm: A computer-based algorithm for Boolean minimization, offering more efficient and accurate results for complex expressions.

• Boolean Algebra: Direct manipulation of Boolean expressions using algebraic rules, though it can be challenging for complex functions.

Q: How can I learn more about Karnaugh maps and digital logic design?

A: Numerous resources are available for learning about Karnaugh maps and digital logic design, including:

• Textbooks: Many textbooks on digital logic design cover Karnaugh maps extensively.

• Online Courses: Numerous online courses and tutorials on digital logic design are readily available on platforms like Coursera, edX, and Udemy.

• Online Resources: Websites like All About Circuits, Electronics Tutorials, and Khan Academy offer comprehensive resources on digital logic design, including Karnaugh maps.

Tips for Effective Karnaugh Map Utilization

• Practice: Familiarity with the construction and manipulation of Karnaugh maps is crucial. Practice with various examples to develop a strong understanding of the concepts.

• Start Simple: Begin with simpler functions and gradually increase the complexity as you gain proficiency.

• Visualize: Utilize visual aids and diagrams to understand the adjacency relationships between cells and the formation of groups.

• Check for Errors: Carefully verify the accuracy of your grouping and the derived expression to avoid errors.

Conclusion: Embracing the Power of Visualization

Karnaugh maps stand as a powerful tool in the digital logic designer’s arsenal, offering a visual and intuitive approach to simplifying complex Boolean expressions. Their ability to exploit adjacency relationships and group minterms efficiently translates to optimized circuit designs with reduced complexity, improved performance, and enhanced readability. While limitations exist for functions with more than five variables, Karnaugh maps remain a valuable technique for simplifying logic and optimizing digital circuits. Understanding and mastering the art of Karnaugh maps empowers designers to create efficient, reliable, and performant digital systems.

Closure

Thus, we hope this article has provided valuable insights into Unraveling Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps. We appreciate your attention to our article. See you in our next article!