The Power of Visual Simplification: Unveiling Boolean Expressions with Karnaugh Maps

Related Articles: The Power of Visual Simplification: Unveiling Boolean Expressions with Karnaugh Maps

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Power of Visual Simplification: Unveiling Boolean Expressions with Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

The Power of Visual Simplification: Unveiling Boolean Expressions with Karnaugh Maps

In the realm of digital logic, Boolean expressions serve as the foundation for representing complex circuits. They utilize logical operators such as AND, OR, and NOT to define the behavior of gates and ultimately, the entire system. However, as the complexity of these expressions grows, deciphering them becomes a challenging task, hindering both understanding and optimization. This is where Karnaugh maps, a visual tool for simplifying Boolean expressions, emerge as a powerful ally.

Understanding Boolean Expressions

Before delving into the intricacies of Karnaugh maps, it is crucial to grasp the fundamentals of Boolean expressions. These expressions are built upon variables, typically representing binary states (0 or 1), and logical operators that define relationships between them.

• AND (·): The AND operator yields a true (1) output only when all its inputs are true. For example, A · B is true only if both A and B are true.
• OR (+): The OR operator yields a true (1) output when at least one of its inputs is true. For example, A + B is true if either A or B or both are true.
• NOT (¬): The NOT operator inverts the input. For example, ¬A is true only if A is false.

These basic operators can be combined to form more complex expressions, representing intricate logic functions. For instance, the expression (A · B) + (¬A · C) describes a circuit that outputs a true value if either both A and B are true or if A is false and C is true.

The Essence of Karnaugh Maps

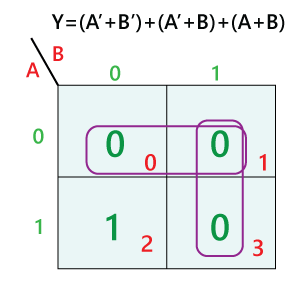
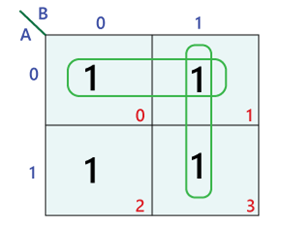
Karnaugh maps, also known as K-maps, are a graphical representation of Boolean expressions. They provide a visual framework for simplifying these expressions by grouping together terms with common characteristics, leading to a more compact and efficient circuit implementation.

The map itself is a grid, with each cell representing a unique combination of input variables. The arrangement of cells is crucial, ensuring that adjacent cells differ by only one variable. This arrangement facilitates the identification of groups of "1" cells, which correspond to terms in the Boolean expression that can be simplified.

Constructing a Karnaugh Map

Creating a Karnaugh map involves several steps:

1. Determining the number of input variables: This dictates the size of the map. For instance, a function with three input variables requires a 2×4 map, while a function with four input variables needs a 4×4 map.
2. Labeling the rows and columns: The rows and columns are labeled with the input variables and their respective values (0 or 1), ensuring that adjacent cells differ by only one variable.
3. Filling the map: Each cell in the map represents a unique combination of input values. The value of the function for that specific combination is then entered into the corresponding cell.

Simplifying Boolean Expressions with Karnaugh Maps

Once the map is populated, the simplification process begins. It involves identifying groups of adjacent cells containing "1" values. These groups must adhere to the following rules:

• Group size: Groups can be of size 1, 2, 4, 8, and so on, representing powers of 2.
• Adjacency: Cells are considered adjacent even if they share a common edge or corner.
• Wrapping: The map is considered to wrap around, meaning that cells on the opposite edges are also considered adjacent.

Each group identified on the map corresponds to a simplified term in the Boolean expression. The process of simplification involves:

• Identifying the variables that are constant within each group: For example, a group spanning four cells where the variable A remains constant at "1" would contribute a term A to the simplified expression.
• Combining these terms using OR operators: The simplified expression is formed by combining all the terms obtained from the identified groups using the OR operator.

Benefits of Using Karnaugh Maps

Employing Karnaugh maps for simplifying Boolean expressions offers several advantages:

• Visual Clarity: The graphical nature of K-maps provides an intuitive way to visualize the relationships between input variables and the output. This visual clarity facilitates understanding and manipulation of complex expressions.
• Efficient Simplification: Grouping "1" cells on the map leads to a more compact and efficient representation of the Boolean expression, resulting in a simpler circuit implementation.
• Reduced Logic Gates: By simplifying the expression, the number of logic gates required to implement the circuit is minimized, leading to cost savings and improved performance.
• Error Prevention: The systematic nature of the map helps prevent errors during simplification, ensuring a more accurate and reliable circuit design.

Beyond Basic Simplification

While Karnaugh maps are primarily used for simplifying Boolean expressions, they can also be employed for other tasks:

• Don’t Care Conditions: In certain scenarios, the output of the function may not be defined for specific input combinations. These "don’t care" conditions can be utilized to further simplify the expression by including them in the groups on the map.
• Product-of-Sums (POS) Form: Karnaugh maps can also be used to derive the product-of-sums (POS) form of a Boolean expression. This involves grouping together the "0" cells on the map and following a similar simplification process.
• Multi-Level Logic: For more complex circuits with multiple levels of logic, Karnaugh maps can be used to simplify each level individually, ultimately leading to a simplified overall circuit design.

FAQs on Karnaugh Maps

1. What is the maximum number of input variables that can be handled by a Karnaugh map?

The maximum number of input variables that can be conveniently handled by a Karnaugh map is five. Beyond that, the map becomes increasingly complex and difficult to manage.

2. How do I handle "don’t care" conditions in a Karnaugh map?

"Don’t care" conditions can be included in groups of "1" cells to further simplify the expression. They are represented by an "X" on the map and can be treated as either "0" or "1" depending on which choice leads to a larger group.

3. Can Karnaugh maps be used for circuits with more than two outputs?

While Karnaugh maps are primarily used for single-output functions, they can be extended to handle multi-output circuits by creating a separate map for each output.

4. Are there any limitations to using Karnaugh maps?

Karnaugh maps become less efficient and practical for functions with a large number of input variables. In such cases, alternative methods like Quine-McCluskey algorithm or Boolean algebra manipulation might be more suitable.

5. Can Karnaugh maps be used for sequential logic circuits?

Karnaugh maps are primarily designed for combinational logic circuits, where the output is solely determined by the current input values. They are not directly applicable to sequential logic circuits, which have memory elements and whose output depends on both current and past inputs.

Tips for Using Karnaugh Maps Effectively

• Start with a clear understanding of the Boolean expression: Before constructing the map, ensure a thorough understanding of the function being represented.
• Choose the appropriate map size: Select the map size based on the number of input variables.
• Label rows and columns carefully: Correctly labeling the rows and columns is crucial for accurate mapping and simplification.
• Identify groups systematically: Use a systematic approach to identify groups, starting with the largest possible groups and working down to smaller ones.
• Consider "don’t care" conditions: Explore the potential benefits of including "don’t care" conditions in your groups.
• Verify the simplified expression: After simplifying the expression, verify its accuracy by comparing it to the original expression.

Conclusion

Karnaugh maps provide a powerful and intuitive tool for simplifying Boolean expressions, enhancing both understanding and optimization of digital circuits. Their visual nature allows for easy identification of common factors and efficient grouping, leading to more compact and efficient circuit designs. While they have their limitations, especially for functions with a large number of input variables, Karnaugh maps remain a valuable technique for simplifying logic circuits and fostering a deeper understanding of Boolean algebra. As the complexity of digital systems continues to evolve, the ability to leverage visual tools like Karnaugh maps will remain crucial for efficient design and implementation.

Closure

Thus, we hope this article has provided valuable insights into The Power of Visual Simplification: Unveiling Boolean Expressions with Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!