The Karnaugh Map: A Visual Tool for Boolean Expression Simplification

Related Articles: The Karnaugh Map: A Visual Tool for Boolean Expression Simplification

Introduction

With great pleasure, we will explore the intriguing topic related to The Karnaugh Map: A Visual Tool for Boolean Expression Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

The Karnaugh Map: A Visual Tool for Boolean Expression Simplification

The Karnaugh map, often referred to as a K-map, is a visual representation of a truth table, providing a powerful tool for simplifying Boolean expressions in digital logic design. This method, developed by Maurice Karnaugh in 1953, is particularly beneficial for minimizing the number of logic gates required to implement a Boolean function, leading to more efficient and cost-effective circuit designs.

Understanding the Karnaugh Map

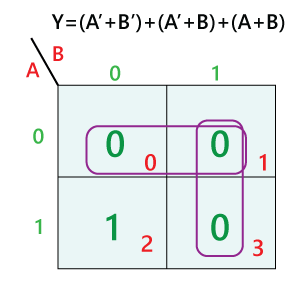
A Karnaugh map is a grid-based diagram where each cell represents a unique combination of input variables. The number of cells in the map corresponds to the total number of possible input combinations, which is 2^n, where ‘n’ is the number of input variables. The cells are arranged in a specific way, ensuring that adjacent cells differ by only one input variable. This arrangement allows for easy identification of adjacent groups of ‘1’s, which represent minterms (product terms) in the Boolean expression.

The map is typically constructed with a binary encoding of the input variables, where each row and column represents a specific combination of variable values. The order of the rows and columns follows a Gray code pattern, where only one bit changes between adjacent cells. This ensures that adjacent cells represent input combinations that differ by only one variable, facilitating the identification of groups of ‘1’s.

Simplifying Boolean Expressions using Karnaugh Maps

The simplification process involves identifying groups of adjacent ‘1’s on the Karnaugh map. These groups represent minterms that can be combined to form simplified product terms. The following rules govern the simplification process:

• Group Size: The size of the group should be a power of two (1, 2, 4, 8, etc.).
• Adjacency: Cells are considered adjacent if they share a common side, even if they wrap around the map.
• Maximum Grouping: Groups should be as large as possible, encompassing the maximum number of ‘1’s.
• Non-Overlapping: Groups should not overlap, although a single ‘1’ can be part of multiple groups.

For each group, the simplified product term is formed by identifying the variables that remain constant within the group and excluding the variables that change. For example, a group of four adjacent ‘1’s in a 4-variable map might represent the simplified product term AB (assuming the variables that remain constant are A and B).

Benefits of Using Karnaugh Maps

The Karnaugh map offers several advantages over traditional algebraic simplification methods:

• Visual Representation: The visual nature of the map makes it easier to understand and identify patterns in the truth table, leading to a more intuitive simplification process.
• Simplified Logic: By identifying and combining adjacent groups of ‘1’s, the Karnaugh map allows for the derivation of simplified Boolean expressions, resulting in fewer logic gates and reduced circuit complexity.
• Systematic Approach: The map provides a structured and systematic method for simplifying Boolean expressions, reducing the risk of errors or omissions.
• Easy to Implement: The map is relatively easy to learn and use, making it a valuable tool for both novice and experienced digital designers.

Applications of Karnaugh Maps

Karnaugh maps find widespread application in various fields, including:

• Digital Logic Design: Minimizing logic circuits for digital systems, reducing cost, power consumption, and complexity.
• Computer Architecture: Optimizing the design of computer components, such as memory controllers and logic units.
• Control Systems: Simplifying control logic for industrial processes and automation systems.
• Digital Signal Processing: Designing filters and other signal processing algorithms.

FAQs

Q: What is the maximum number of variables that can be represented by a Karnaugh map?

A: The maximum number of variables that can be represented by a Karnaugh map is limited by the number of cells it can accommodate. For practical purposes, maps with up to six variables are commonly used.

Q: How do I handle "don’t care" conditions in a Karnaugh map?

A: "Don’t care" conditions, denoted by ‘X’ in the map, represent input combinations that are not relevant to the desired output. These conditions can be used to simplify the expression by including them in groups of ‘1’s, as long as they do not affect the overall function.

Q: What are the limitations of Karnaugh maps?

A: While powerful, Karnaugh maps have limitations for larger circuits with many variables. For functions with more than six variables, the map becomes too complex to handle effectively. Additionally, the map is not as suitable for simplifying expressions with multiple outputs.

Tips for Using Karnaugh Maps

• Start with a Truth Table: Construct a truth table for the given Boolean function before creating the Karnaugh map.
• Choose the Right Map Size: Select a map with the appropriate number of cells to represent the input variables.
• Label Rows and Columns: Use binary encoding for rows and columns, following the Gray code pattern.
• Identify Groups: Carefully identify all possible groups of adjacent ‘1’s, ensuring they are as large as possible.
• Write Simplified Expressions: For each group, write down the simplified product term by identifying the constant variables.
• Combine Terms: Combine the simplified product terms using OR operations to form the final simplified expression.

Conclusion

The Karnaugh map is a powerful and versatile tool for simplifying Boolean expressions in digital logic design. Its visual nature and systematic approach make it a valuable asset for designing efficient and cost-effective circuits. While limitations exist for larger circuits, the Karnaugh map remains an essential technique for digital design students and professionals alike. By understanding its principles and mastering its application, engineers can significantly enhance the design and optimization of digital systems.

Closure

Thus, we hope this article has provided valuable insights into The Karnaugh Map: A Visual Tool for Boolean Expression Simplification. We hope you find this article informative and beneficial. See you in our next article!