Navigating Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

Related Articles: Navigating Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

Introduction

With great pleasure, we will explore the intriguing topic related to Navigating Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

Navigating Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps

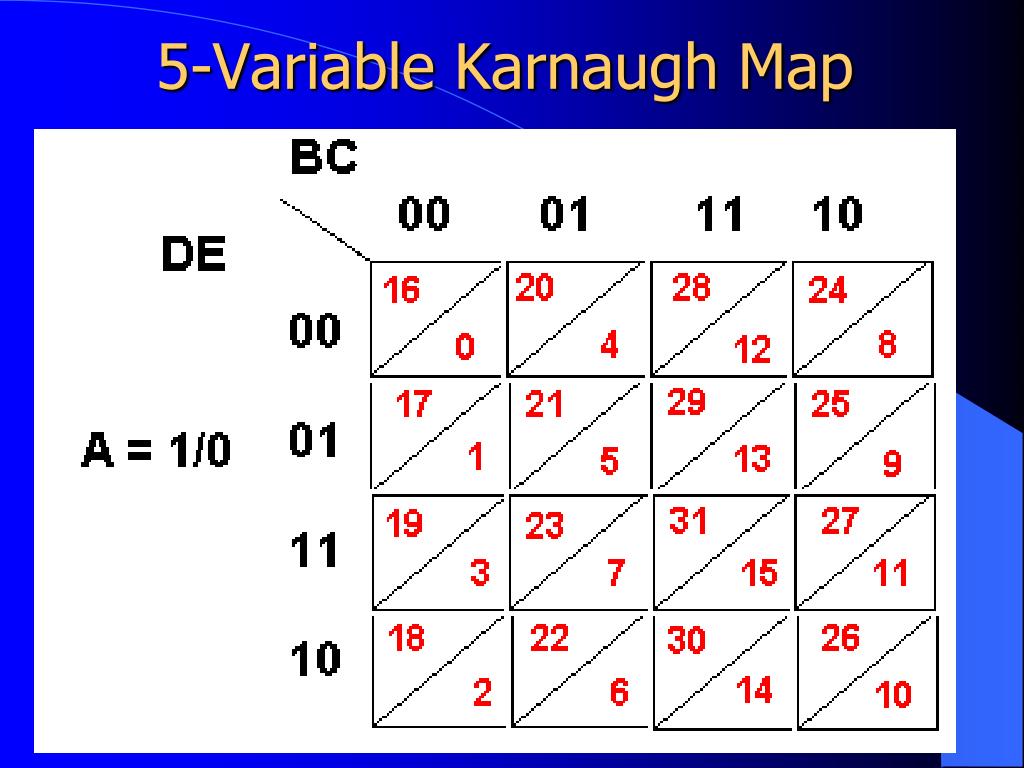
The realm of digital logic design thrives on the ability to translate complex Boolean expressions into efficient hardware implementations. One of the most powerful tools in this process is the Karnaugh map (K-map), a visual representation that simplifies Boolean algebra and aids in deriving minimal sum-of-products (SOP) or product-of-sums (POS) expressions. While 2, 3, and 4-variable K-maps are readily visualized, tackling a 5-variable K-map requires a slightly different approach, leveraging the power of three-dimensional representation and a systematic understanding of its principles.

Understanding the Foundation: A Primer on Karnaugh Maps

At its core, a K-map is a graphical representation of a truth table, where each cell corresponds to a unique combination of input variables. The arrangement of cells is not arbitrary; it follows a Gray code pattern, ensuring that adjacent cells differ by only one input variable. This arrangement facilitates the identification of groups of adjacent ‘1’ cells, which represent logical terms that can be combined to simplify the Boolean expression.

Visualizing the Fifth Dimension: The 5-Variable K-Map

The challenge with 5-variable K-maps lies in representing five variables on a two-dimensional plane. The solution lies in visualizing the map as a three-dimensional structure, where the fifth variable acts as a "layer" or "slice." A typical 5-variable K-map is often represented as two 4-variable K-maps, one representing the ‘0’ state of the fifth variable and the other representing the ‘1’ state. This visual separation helps in recognizing groups of ‘1’ cells across the layers, leading to the simplification of the expression.

Navigating the 5-Variable Landscape: A Step-by-Step Approach

1. Defining the Variables: Clearly identify the five input variables and their corresponding truth table values (0 or 1).

2. Constructing the 3D Structure: Visualize two 4-variable K-maps, one for each state of the fifth variable. Label the rows and columns of each map with the appropriate variable combinations, adhering to the Gray code pattern.

3. Mapping the Function: For each row of the truth table, locate the corresponding cell in the appropriate 4-variable K-map (based on the fifth variable’s value). If the output for that row is ‘1’, mark the cell with a ‘1’.

4. Grouping the ‘1’ Cells: Identify groups of adjacent ‘1’ cells across both 4-variable K-maps. A group can be formed horizontally, vertically, or even across the two layers, as long as the cells differ by only one variable. The size of the group should be as large as possible, always a power of 2.

5. Writing the Simplified Expression: For each group, write down the logical term corresponding to the variables that remain constant within the group. For example, a group covering all cells where ‘A’ and ‘B’ are ‘1’ and ‘C’, ‘D’, and ‘E’ vary would be represented by ‘A.B’.

6. Final Expression: Combine the logical terms for all groups using the OR operator to obtain the minimal SOP expression.

Beyond the Basics: Advanced Considerations

1. Don’t Care Conditions: In some cases, certain input combinations may not be relevant to the function’s operation. These "don’t care" conditions are marked as ‘X’ in the K-map. These ‘X’ cells can be strategically included in groups to further simplify the expression.

2. Product-of-Sums (POS): While SOP is the most common form, K-maps can also be used to derive minimal POS expressions. In this case, the focus shifts to grouping ‘0’ cells instead of ‘1’ cells. The resulting expression will be a product of sum terms, where each sum term represents a group of ‘0’ cells.

Frequently Asked Questions

1. What are the limitations of 5-variable K-maps?

While powerful, 5-variable K-maps become increasingly complex to visualize and manage. For larger numbers of variables (6 or more), alternative methods like Quine-McCluskey algorithm or Boolean algebra manipulation become more efficient.

2. Can K-maps be used for functions with multiple outputs?

Yes, K-maps can be used for functions with multiple outputs. A separate K-map is required for each output, and the simplification process is performed independently for each map.

3. Are there any software tools available to help with K-map simplification?

Numerous software tools and online calculators are available to simplify Boolean expressions and visualize K-maps, even for 5-variable functions. These tools can automate the grouping process and provide a more intuitive representation of the 3D structure.

Tips for Effective K-Map Usage

1. Start with a Clear Truth Table: A well-organized truth table is essential for accurate mapping onto the K-map.

2. Practice with Smaller Examples: Begin with 2, 3, and 4-variable K-maps to solidify your understanding before tackling 5-variable maps.

3. Use Visual Aids: Draw the K-map structure clearly and use different colors or symbols to differentiate groups of ‘1’ cells.

4. Consider Don’t Cares: Strategic use of "don’t cares" can lead to significant simplification.

5. Verify Your Results: After obtaining a simplified expression, use Boolean algebra or a truth table to verify its correctness.

Conclusion: A Powerful Tool for Logic Design

The 5-variable K-map, despite its three-dimensional nature, remains a valuable tool for simplifying Boolean expressions and designing efficient digital circuits. Its visual representation allows for intuitive identification of logical terms and provides a pathway to minimize the complexity of logic functions. By understanding the principles of K-map construction and simplification, engineers and designers can effectively leverage this powerful tool to streamline their design process and create robust, optimized digital systems.

Closure

Thus, we hope this article has provided valuable insights into Navigating Complexity: A Comprehensive Guide to 5-Variable Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!