Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to 4-Variable Optimization

Related Articles: Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to 4-Variable Optimization

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to 4-Variable Optimization. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to 4-Variable Optimization

The realm of digital logic design thrives on efficient and effective manipulation of Boolean expressions. Central to this endeavor is the Karnaugh map (K-map), a visual tool that empowers simplification of complex Boolean functions. While K-maps can be applied to any number of variables, this exploration delves into the practical and insightful use of 4-variable K-maps, illuminating their significance in minimizing logic circuits and optimizing digital designs.

Understanding the Fundamentals of K-Maps

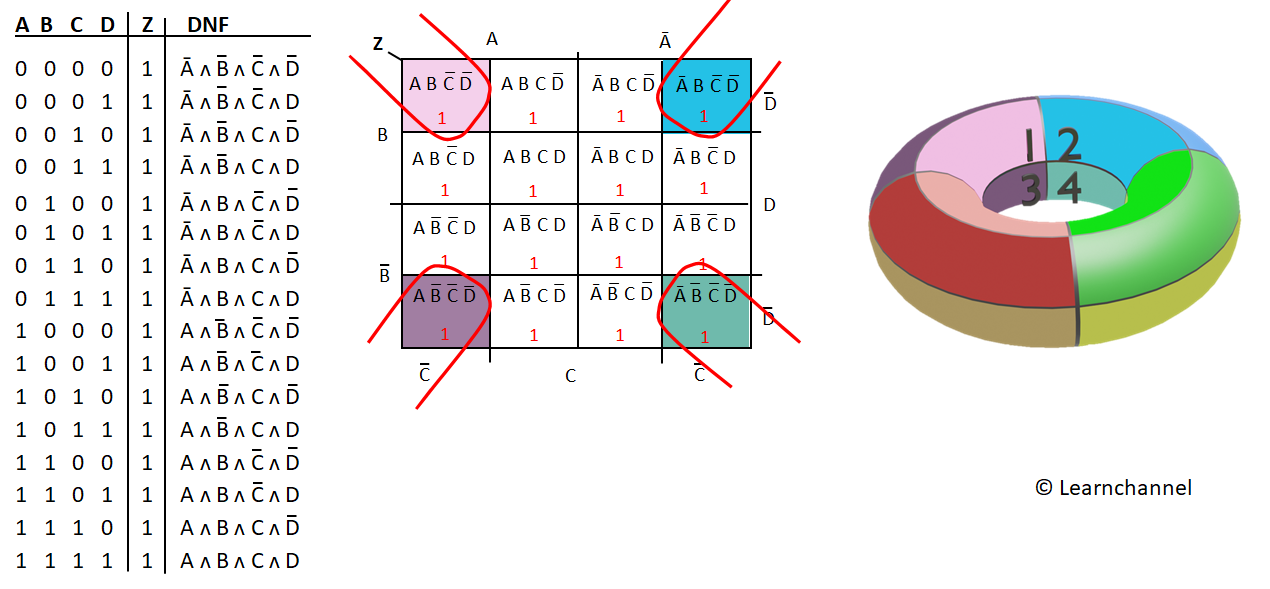
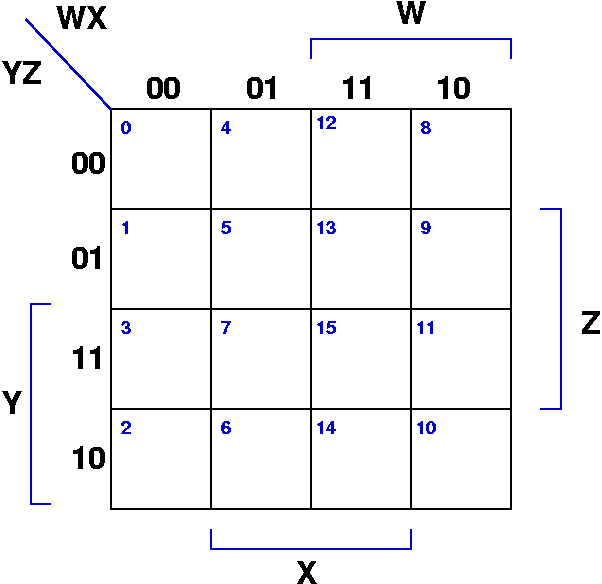
A K-map is essentially a graphical representation of a truth table, cleverly arranged to facilitate the identification of adjacent minterms (product terms) that can be combined to form simpler expressions. The map’s structure is based on a binary arrangement, with each cell representing a unique combination of input variables. For a 4-variable K-map, there are 16 cells, corresponding to the 16 possible combinations of four variables.

The Key to Simplification: Adjacency and Grouping

The magic of K-maps lies in their ability to visually highlight the relationships between adjacent minterms. Two minterms are considered adjacent if their binary representations differ by only one bit. This adjacency is crucial because it allows for the application of Boolean algebra’s key property:

• A + A’ = 1

When two adjacent minterms are grouped, the variable that differs between them is eliminated, leading to a simplified expression. The goal is to group the 1s (representing minterms where the function evaluates to true) in the K-map into the largest possible rectangular groups, always ensuring that the groups contain a power of two number of cells.

Constructing a 4-Variable K-Map

To construct a 4-variable K-map, the four input variables (typically denoted as A, B, C, and D) are assigned to the rows and columns of the map. The rows are arranged in a Gray code sequence, where only one bit changes between consecutive rows. Similarly, the columns follow a Gray code sequence. This arrangement ensures that adjacent cells represent minterms that differ by only one variable.

Illustrative Example: Simplifying a 4-Variable Boolean Function

Consider the Boolean function:

F(A, B, C, D) = Σm(0, 2, 4, 6, 8, 10, 12, 14)

This expression represents a function that evaluates to true for the minterms 0, 2, 4, 6, 8, 10, 12, and 14. To simplify this function using a K-map:

1. Create the K-map: Place a 1 in the cells corresponding to the minterms where the function evaluates to true.

2. Identify groups: Group the 1s into the largest possible rectangles, ensuring that each group contains a power of two number of cells.

3. Write the simplified expression: For each group, identify the variables that are constant within the group and form a product term.

In this example, the K-map reveals several groups:

• A group of eight cells encompassing all the minterms, resulting in the term ‘1’.

• A group of four cells with A’B’ as the constant term.

• A group of two cells with A’CD’ as the constant term.

Therefore, the simplified expression for F(A, B, C, D) becomes:

F(A, B, C, D) = 1 + A’B’ + A’CD’

Benefits of Using K-Maps for 4-Variable Functions

The use of K-maps for 4-variable functions offers several significant advantages:

• Visual simplification: K-maps provide a visual representation of the function, making it easier to identify and group adjacent minterms.

• Reduced complexity: The graphical approach significantly simplifies the process of simplifying Boolean expressions, particularly for functions with a large number of variables.

• Enhanced understanding: K-maps offer a deeper understanding of the relationships between minterms and their impact on the function’s output.

• Efficiency in circuit design: By minimizing the Boolean expressions, K-maps contribute to the design of simpler and more efficient logic circuits, reducing the number of gates required and minimizing power consumption.

FAQs about K-Map Calculators for 4-Variable Functions

Q: What are the limitations of K-maps?

A: While K-maps are powerful tools, they become cumbersome and less effective for functions with more than five variables. For higher-order functions, alternative methods like Quine-McCluskey algorithm or algebraic manipulation are more suitable.

Q: How can I use a K-map calculator to simplify a 4-variable function?

A: K-map calculators are online tools that automate the process of creating and simplifying K-maps. They typically require users to input the minterms for which the function evaluates to true. The calculator then generates the K-map, identifies the optimal groups, and provides the simplified Boolean expression.

Q: What are some tips for using K-maps effectively?

A:

• Start with the largest groups: Begin by identifying the largest possible groups of 1s in the K-map.

• Look for overlapping groups: Groups can overlap, and this overlap should be considered when forming the simplified expression.

• Use Gray code: Ensure that the rows and columns of the K-map follow a Gray code sequence for accurate adjacency representation.

• Check for Don’t Cares: If certain input combinations are not relevant to the function, they are represented as "Don’t Cares" (represented by X) and can be used to form larger groups.

Conclusion

The Karnaugh map, particularly in its 4-variable form, stands as a cornerstone of digital logic design. Its ability to visually simplify complex Boolean expressions, reduce circuit complexity, and enhance understanding makes it an indispensable tool for engineers and designers. By mastering the art of constructing and interpreting K-maps, one can navigate the intricate world of Boolean functions with confidence, paving the way for efficient and optimized digital systems.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Power of Karnaugh Maps: A Comprehensive Guide to 4-Variable Optimization. We hope you find this article informative and beneficial. See you in our next article!