Demystifying the 6-Variable Karnaugh Map: A Comprehensive Guide

Related Articles: Demystifying the 6-Variable Karnaugh Map: A Comprehensive Guide

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the 6-Variable Karnaugh Map: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the 6-Variable Karnaugh Map: A Comprehensive Guide

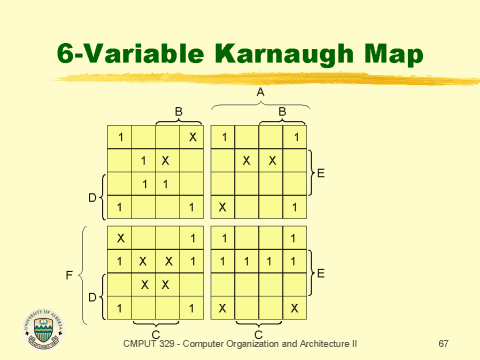
The realm of digital circuit design relies heavily on the efficient manipulation of Boolean expressions. These expressions, representing logical relationships between binary inputs and outputs, form the foundation for complex digital systems. One powerful tool employed in this domain is the Karnaugh Map (K-map), a graphical method for simplifying Boolean expressions and deriving optimal logic circuits. While K-maps are traditionally used for expressions with up to four variables, their application extends to higher dimensions, albeit with increased complexity. This article delves into the intricacies of 6-variable K-maps, exploring their construction, application, and the advantages they offer in simplifying complex Boolean expressions.

Understanding the Basics: K-Maps and Boolean Algebra

Before diving into the intricacies of 6-variable K-maps, it’s essential to grasp the fundamental principles of K-maps and their relationship with Boolean algebra.

Boolean Algebra is a mathematical system that deals with binary values (0 and 1) and logical operations such as AND, OR, and NOT. These operations are represented by symbols like:

• AND: ‘.’ or ‘∧’ (e.g., A . B or A ∧ B)
• OR: ‘+’ or ‘∨’ (e.g., A + B or A ∨ B)
• NOT: ‘¬’ or ‘!’ (e.g., ¬A or !A)

Karnaugh Maps are visual representations of truth tables, providing a structured approach for simplifying Boolean expressions. They are essentially grids where each cell corresponds to a unique combination of input variables. The arrangement of cells is crucial; adjacent cells differ by only one variable, facilitating the identification of groups of ‘1’s (representing ‘true’ outputs) that can be combined into simplified Boolean expressions.

The Challenge of 6-Variable K-Maps

While K-maps are a valuable tool for simplifying Boolean expressions, their effectiveness diminishes as the number of variables increases. This is because the size and complexity of the K-map escalate exponentially. A 6-variable K-map requires a 64-cell grid, making it challenging to visualize and manipulate.

Constructing a 6-Variable K-Map

Despite the complexity, constructing a 6-variable K-map follows a systematic approach:

1. Variable Arrangement: The six input variables are assigned to the rows and columns of the map. The most common arrangement is a Gray code ordering, where adjacent cells differ by only one variable.
2. Cell Representation: Each cell represents a unique combination of input variables, with the row and column values determining the binary representation of the input.
3. Truth Table Mapping: The truth table of the Boolean expression is used to populate the K-map. A ‘1’ is placed in the cell corresponding to the input combination that results in a ‘1’ output, and a ‘0’ is placed for input combinations resulting in a ‘0’ output.

Simplifying Boolean Expressions with 6-Variable K-Maps

The core principle of using K-maps to simplify Boolean expressions is to identify groups of adjacent cells containing ‘1’s. These groups are called prime implicants, and they represent simplified terms in the Boolean expression. The goal is to cover all ‘1’s in the K-map using the fewest possible prime implicants.

Key Rules for Identifying Prime Implicants:

• Adjacency: Cells are considered adjacent if they differ in only one variable. This includes cells that are physically adjacent and cells that are at the opposite edges of the map (due to the Gray code arrangement).
• Group Size: Prime implicants should be as large as possible, containing a power of two number of cells (2, 4, 8, 16, etc.).
• Essential Prime Implicants: Some prime implicants cover ‘1’s that cannot be covered by any other prime implicant. These are called essential prime implicants and must be included in the simplified expression.

Example:

Consider a Boolean expression with six variables:

F(A, B, C, D, E, F) = Σm(0, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63)

This expression represents a function with 64 possible input combinations, all resulting in a ‘1’ output. When mapped onto a 6-variable K-map, this would result in all cells being filled with ‘1’s. Therefore, the simplified expression is simply:

F(A, B, C, D, E, F) = 1

This example demonstrates how a K-map can reveal an extremely simple expression, even for a complex function.

Advantages of Using 6-Variable K-Maps

While the complexity of 6-variable K-maps might seem daunting, they offer significant advantages in simplifying Boolean expressions:

• Reduced Circuit Complexity: Simplifying Boolean expressions using K-maps leads to fewer logic gates in the final circuit, reducing cost, size, and power consumption.
• Improved Performance: Simplified circuits often exhibit faster switching speeds and lower propagation delays, enhancing the overall performance of the digital system.
• Enhanced Maintainability: Simplified expressions are easier to understand and modify, making the circuit design more maintainable and adaptable.

FAQs on 6-Variable K-Maps

1. What are the limitations of 6-variable K-maps?

While powerful, 6-variable K-maps become increasingly challenging to manage due to their size and complexity. Beyond six variables, the visualization and manipulation become impractical, requiring alternative simplification methods like Quine-McCluskey algorithm.

2. How can I effectively use a 6-variable K-map?

Practice and familiarity are key. Start with simpler examples and gradually increase the complexity. Utilize tools like online K-map calculators to assist in visualization and simplification.

3. Are there any alternatives to using 6-variable K-maps?

For expressions with more than six variables, the Quine-McCluskey algorithm offers a more systematic and algorithmic approach to simplification.

Tips for Using 6-Variable K-Maps

• Break Down Complexity: Divide the 6-variable K-map into smaller sections, focusing on simplifying each section independently.
• Utilize Symmetry: Look for patterns and symmetries in the K-map to identify groups of adjacent cells more easily.
• Use Online Tools: Online K-map calculators can help visualize the map and identify prime implicants.

Conclusion

The 6-variable Karnaugh map is a powerful tool for simplifying complex Boolean expressions, leading to optimized digital circuits with reduced complexity, improved performance, and enhanced maintainability. While its application requires a thorough understanding of Boolean algebra and the intricacies of K-map construction, the benefits it offers in simplifying logic circuits are undeniable. As digital systems continue to grow in complexity, tools like 6-variable K-maps remain crucial for efficient and effective circuit design.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the 6-Variable Karnaugh Map: A Comprehensive Guide. We appreciate your attention to our article. See you in our next article!