Demystifying the 4-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Related Articles: Demystifying the 4-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the 4-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the 4-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

The realm of digital logic is built upon the foundation of Boolean algebra, a system that utilizes binary values (0 and 1) to represent logical operations. One of the fundamental tools for simplifying Boolean expressions and designing digital circuits is the Karnaugh map, often referred to as a K-map. This article delves into the intricacies of the 4-variable Karnaugh map, providing a detailed exploration of its construction, application, and significance in digital design.

Understanding the Fundamentals: Boolean Algebra and Logic Gates

Before delving into the specifics of the 4-variable K-map, it is essential to grasp the core concepts of Boolean algebra and logic gates. Boolean algebra forms the mathematical framework for digital logic, employing variables representing logical states (true or false) and operators like AND, OR, and NOT to manipulate these states.

• AND Gate: The AND gate outputs a 1 only when all its inputs are 1.
• OR Gate: The OR gate outputs a 1 if at least one of its inputs is 1.
• NOT Gate: The NOT gate inverts the input, transforming a 1 to a 0 and vice versa.

These fundamental logic gates are the building blocks of complex digital circuits. Boolean expressions, which represent the logical behavior of these circuits, can be simplified using techniques like the Karnaugh map.

The Karnaugh Map: A Visual Tool for Boolean Simplification

The Karnaugh map is a graphical representation of a Boolean function, enabling straightforward simplification by visually identifying and grouping adjacent minterms (products of literals). Each cell in the map corresponds to a unique combination of input variables. The arrangement of cells follows a specific pattern that ensures adjacent cells differ in only one variable.

Construction of a 4-Variable Karnaugh Map

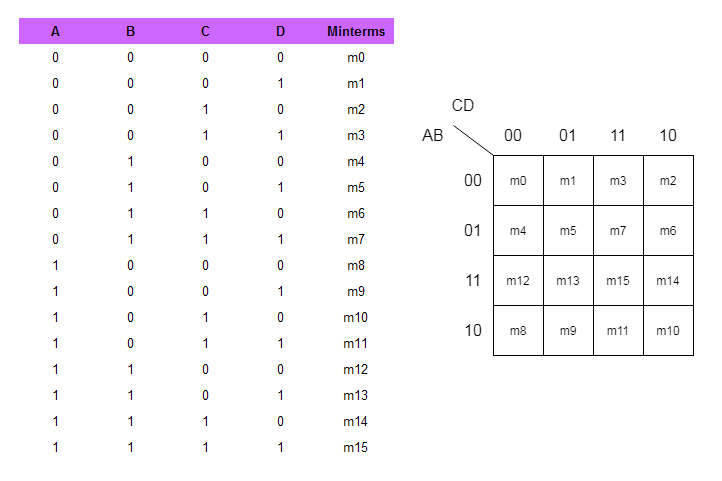
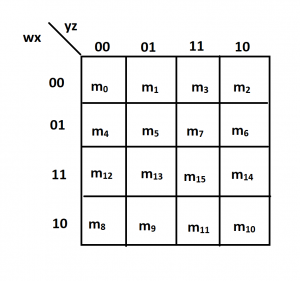
A 4-variable Karnaugh map consists of 16 cells, representing all possible combinations of four input variables (A, B, C, D). The map is arranged in a grid format with rows representing the combinations of variables C and D, and columns representing the combinations of variables A and B. The order of variables in the columns and rows follows the Gray code, where only one bit changes between adjacent cells.

Gray Code: Ensuring Adjacency

The Gray code is crucial in Karnaugh map construction. It ensures that adjacent cells differ by only one variable, enabling the identification of adjacent minterms for simplification. In the 4-variable K-map, the Gray code sequence for the columns is 00, 01, 11, 10, and for the rows is 00, 01, 11, 10.

Mapping Boolean Functions onto the Karnaugh Map

To use the Karnaugh map, we map the Boolean function onto it by placing a ‘1’ in each cell corresponding to a minterm that evaluates to ‘1’ for the function. The remaining cells are filled with ‘0’s.

Simplification through Grouping

The key to simplifying Boolean expressions using the Karnaugh map lies in grouping adjacent cells containing ‘1’s. These groups must be rectangular or square in shape, and their size should be a power of two (1, 2, 4, 8). Each group represents a simplified product term in the minimized expression.

Rules for Grouping:

• Adjacency: Cells are considered adjacent if they share a common edge. This includes cells on the opposite edges of the map, as they are considered adjacent due to the Gray code arrangement.
• Power of Two: The number of cells in each group must be a power of two.
• Maximize Group Size: Larger groups lead to simpler terms, so aim to create the largest possible groups.
• Don’t Care Conditions: Sometimes, certain input combinations are not relevant to the function. These are denoted by ‘X’ on the map and can be included in groups to further simplify the expression.

Obtaining the Minimized Expression

Once the groups are formed, the minimized Boolean expression is derived by identifying the variables that are common to all cells within each group. For a variable that remains constant (0 or 1) within the group, its corresponding literal is included in the product term. If a variable changes within the group, it is omitted.

Example: Simplifying a 4-Variable Boolean Expression

Consider the following Boolean function:

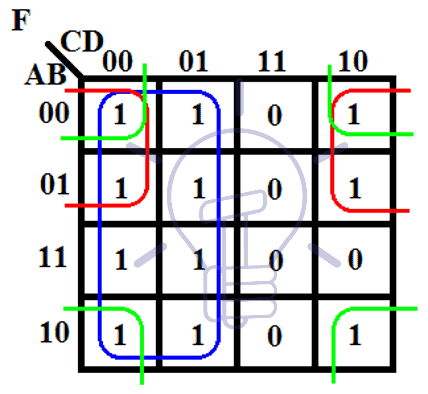
F(A, B, C, D) = Σm(0, 2, 4, 6, 8, 10, 12, 14)

This function is represented by the sum of minterms (Σm) where the minterms are specified by their decimal indices (0, 2, 4, 6, 8, 10, 12, 14). To simplify this function, we map it onto a 4-variable Karnaugh map:

[Insert a visual representation of the 4-variable Karnaugh map with the minterms marked as ‘1’s.]

By grouping the adjacent cells containing ‘1’s, we obtain the following simplified expression:

F(A, B, C, D) = A'C' + A'D' + BD

Benefits of Using the Karnaugh Map

The Karnaugh map offers significant advantages in simplifying Boolean expressions:

• Visual Representation: It provides a visual representation of the Boolean function, making it easier to identify patterns and simplify expressions.
• Straightforward Simplification: The process of grouping adjacent cells is intuitive and straightforward.
• Minimized Expressions: The Karnaugh map consistently yields minimized expressions, leading to simpler and more efficient digital circuits.
• Don’t Care Conditions: It allows for the inclusion of don’t care conditions, further simplifying the expressions.

Applications of the 4-Variable Karnaugh Map

The 4-variable Karnaugh map finds widespread application in various digital design contexts:

• Logic Circuit Design: It is used to simplify Boolean expressions representing logic circuits, resulting in more efficient and cost-effective designs.
• Digital System Optimization: It helps optimize digital systems by reducing the number of gates and simplifying the overall logic, leading to improved performance and reduced power consumption.
• Combinational Circuit Design: The Karnaugh map is a powerful tool for designing and analyzing combinational circuits, where the output is a function of the current input only.
• Sequential Circuit Design: It can also be used in the design of sequential circuits, where the output depends on both the current input and the past state of the circuit.

FAQs Regarding the 4-Variable Karnaugh Map

Q1: What is the maximum number of variables that can be represented using a Karnaugh map?

A1: While Karnaugh maps can be used for up to 5 variables, their effectiveness diminishes beyond 4 variables due to the complexity of the map’s structure. For higher numbers of variables, other simplification techniques like Quine-McCluskey method are employed.

Q2: How do I handle don’t care conditions in a Karnaugh map?

A2: Don’t care conditions are represented by ‘X’ in the Karnaugh map. They can be included in groups to further simplify the expression. The choice of including or excluding a don’t care condition depends on the desired output for the corresponding input combination.

Q3: What happens if there are multiple possible groupings in a Karnaugh map?

A3: If multiple groupings are possible, the choice of grouping depends on the desired level of simplification. Larger groups generally lead to simpler expressions, but they might not always be feasible due to the map’s structure.

Q4: Can I use a Karnaugh map to simplify expressions with more than 4 variables?

A4: While the standard Karnaugh map is designed for up to 4 variables, there are variations for 5 variables. However, for higher numbers of variables, alternative techniques like the Quine-McCluskey method are more efficient.

Tips for Using the 4-Variable Karnaugh Map

• Start with a Clear Map: Ensure the map is accurately constructed with the correct arrangement of variables and cells.
• Identify Adjacent Cells: Carefully identify all adjacent cells containing ‘1’s, including those on the opposite edges of the map.
• Maximize Group Size: Aim to create the largest possible groups while adhering to the power-of-two rule.
• Consider Don’t Care Conditions: Utilize don’t care conditions strategically to further simplify the expression.
• Check for Redundant Terms: After obtaining the simplified expression, verify if any terms are redundant and can be removed.

Conclusion: The 4-Variable Karnaugh Map – A Powerful Tool for Digital Design

The 4-variable Karnaugh map is a fundamental tool in digital design, enabling the simplification of Boolean expressions and the optimization of digital circuits. Its visual nature and straightforward approach make it an invaluable resource for logic circuit design and analysis. By understanding the construction, application, and benefits of the Karnaugh map, engineers and designers can effectively simplify Boolean functions, leading to efficient, cost-effective, and reliable digital systems.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the 4-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification. We appreciate your attention to our article. See you in our next article!