Demystifying the 3-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Related Articles: Demystifying the 3-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying the 3-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the 3-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification

The realm of digital logic design relies heavily on simplifying complex Boolean expressions. While truth tables provide a systematic representation of logical functions, they often fail to offer an intuitive understanding of potential simplifications. This is where the Karnaugh map, a visual tool, steps in, offering a powerful and efficient method for minimizing Boolean expressions. Among its variations, the 3-variable Karnaugh map stands out as a fundamental tool for students and professionals alike, enabling the optimization of digital circuits.

Understanding the Basics

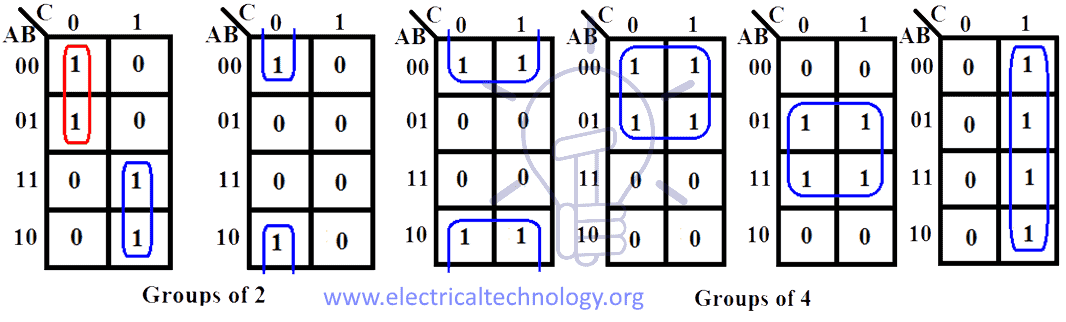
A Karnaugh map is a graphical representation of a Boolean function, where each cell corresponds to a unique combination of input variables. The arrangement of cells adheres to a specific pattern, ensuring that adjacent cells differ by only one variable. This property allows for the identification of groups of adjacent ‘1’s, which represent terms that can be combined and simplified.

In a 3-variable Karnaugh map, the three variables (typically labeled A, B, and C) are represented along the edges of a 2×4 grid. The rows and columns are assigned binary values, with each cell representing a unique combination of these values. For instance, the cell at the intersection of row ’01’ and column ’10’ corresponds to the input combination A=0, B=1, and C=0.

The Power of Adjacency

The key to simplifying Boolean expressions using a Karnaugh map lies in recognizing the adjacency of ‘1’s. Adjacent cells, either horizontally or vertically, represent terms that differ by only one variable. This difference can be eliminated during simplification, leading to a more concise expression.

For example, if two adjacent cells contain ‘1’s, they represent terms like ‘AB’ and ‘AB’. These terms can be combined to form ‘A’, eliminating the variable ‘B’. This simplification process continues until all ‘1’s are grouped into the largest possible adjacent blocks, each representing a simplified term.

Interpreting the Map

Once the ‘1’s are grouped into blocks, each block corresponds to a simplified term in the Boolean expression. The simplified term is determined by identifying the variables that remain constant within the block. For example, a block encompassing the cells ‘010’, ‘011’, ‘110’, and ‘111’ represents the term ‘B’. This term is obtained by observing that the variable ‘B’ is constant (equal to ‘1’) within the block, while the variables ‘A’ and ‘C’ vary.

Illustrative Example

Let’s consider a 3-variable Boolean function represented by the following truth table:

A	B	C	F
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

To simplify this function using a 3-variable Karnaugh map, we first populate the map with ‘1’s corresponding to the rows where the output ‘F’ is ‘1’. The resulting map is as follows:

     AB
     00 01 11 10
C 0 | 0  1  0  1
  1 | 1  0  1  1

Analyzing the map, we identify two groups of adjacent ‘1’s:

• A group of two ‘1’s in the top row, representing the term ‘C’.
• A group of four ‘1’s encompassing the last two columns, representing the term ‘A’.

Therefore, the simplified Boolean expression for the given function is:

F = A + C

Benefits of Using Karnaugh Maps

The use of Karnaugh maps offers several advantages over traditional Boolean simplification methods:

• Visual Clarity: Karnaugh maps provide a visual representation of the Boolean function, making it easier to identify potential simplifications.
• Intuitive Approach: The process of grouping adjacent ‘1’s is intuitive and straightforward, even for beginners.
• Efficiency: Karnaugh maps offer a faster and more efficient way to simplify Boolean expressions compared to algebraic methods.
• Error Reduction: The visual nature of Karnaugh maps reduces the likelihood of errors during simplification.
• Comprehensive Simplification: Karnaugh maps can handle complex Boolean expressions with multiple variables, leading to optimal simplification.

FAQs

Q: What is the maximum number of variables that can be represented using a Karnaugh map?

A: The number of variables that can be represented using a Karnaugh map depends on the complexity of the map. For practical purposes, Karnaugh maps are typically used for up to 5 variables. Beyond this, the map becomes too complex and difficult to manage.

Q: Can Karnaugh maps be used to simplify expressions with "don’t care" conditions?

A: Yes, Karnaugh maps can effectively handle "don’t care" conditions. These conditions represent input combinations where the output value is irrelevant. In the Karnaugh map, ‘don’t cares’ are represented by ‘X’ and can be included in any group to maximize simplification.

Q: What are the limitations of using Karnaugh maps?

A: While Karnaugh maps are a powerful tool, they have certain limitations:

• Complexity: For functions with more than five variables, the map becomes too complex to use effectively.
• Limited Scope: Karnaugh maps are primarily used for simplification, not for designing complex circuits.
• Potential for Error: While intuitive, there’s a possibility of overlooking potential simplifications or making errors in grouping ‘1’s.

Tips for Using Karnaugh Maps Effectively

• Start with a Clear Truth Table: Ensure the truth table accurately represents the Boolean function before mapping it onto the Karnaugh map.
• Label the Rows and Columns Correctly: Maintain the binary order of the rows and columns to ensure proper adjacency of cells.
• Identify the Largest Blocks: Aim to group the ‘1’s into the largest possible blocks, maximizing simplification.
• Use "Don’t Cares" Strategically: Include "don’t cares" in groups to further simplify the expression.
• Check for Completeness: Verify that all ‘1’s are included in at least one group to ensure complete simplification.

Conclusion

The 3-variable Karnaugh map is an indispensable tool for simplifying Boolean expressions, offering a visual and intuitive approach to optimize digital circuits. By understanding the principles of adjacency and grouping, users can effectively minimize expressions, reducing the complexity of circuits and improving their efficiency. While Karnaugh maps have limitations, their effectiveness in simplifying Boolean expressions for functions with up to five variables makes them an invaluable tool for students and professionals alike, contributing significantly to the advancement of digital logic design.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the 3-Variable Karnaugh Map: A Comprehensive Guide to Boolean Simplification. We hope you find this article informative and beneficial. See you in our next article!