Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Three Variables

Related Articles: Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Three Variables

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Three Variables. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Three Variables

The realm of digital circuits and logic design often involves complex Boolean expressions that can be challenging to simplify. Enter Karnaugh maps, a powerful visual tool that simplifies the process of minimizing Boolean expressions, leading to more efficient and cost-effective circuits. This article delves into the intricacies of Karnaugh maps, specifically focusing on their application for three variables, offering a comprehensive understanding of their functionality and benefits.

Understanding the Fundamentals: What are Karnaugh Maps?

Karnaugh maps, often referred to as K-maps, are graphical representations of Boolean functions. They provide a systematic method for simplifying Boolean expressions by identifying and combining adjacent minterms (product terms) that share common variables. Each cell in the map corresponds to a unique combination of input variables, and the value assigned to each cell represents the output of the Boolean function for that specific input combination.

The Three-Variable Karnaugh Map: Visualizing Complexity

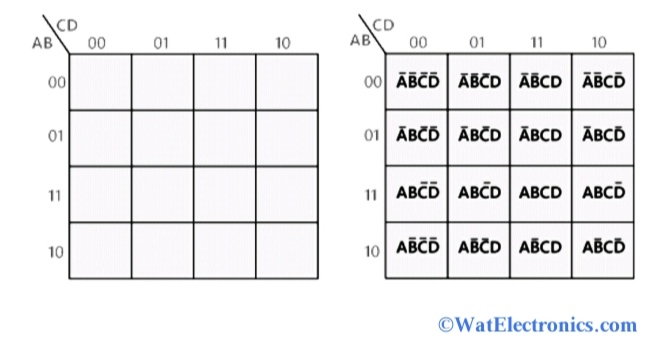
A three-variable Karnaugh map is a 2×4 grid, where each row and column represents a different combination of input variables. The arrangement of the rows and columns follows a specific pattern, ensuring that adjacent cells differ by only one variable. This strategic arrangement is crucial for identifying groups of adjacent minterms that can be combined for simplification.

Here’s a breakdown of the three-variable K-map:

• Rows: Represent the first two variables (e.g., A and B), with each row representing a unique combination of these variables (00, 01, 11, 10).
• Columns: Represent the third variable (e.g., C), with each column representing a unique value of C (0, 1).
• Cells: Each cell in the map represents a unique combination of all three input variables.

Mapping Boolean Functions: A Step-by-Step Approach

To use a Karnaugh map, you need to map the given Boolean function onto the grid. This involves assigning a "1" to the cells corresponding to the input combinations that produce a "1" output and a "0" to the cells representing input combinations that produce a "0" output.

Here’s a step-by-step guide to mapping a Boolean function onto a three-variable K-map:

1. Identify the input variables: Determine the variables involved in the Boolean function.
2. Create the K-map: Draw a 2×4 grid, labeling the rows and columns with the input variables as described above.
3. Assign values to the cells: For each input combination, evaluate the Boolean function and assign a "1" or "0" to the corresponding cell in the K-map.
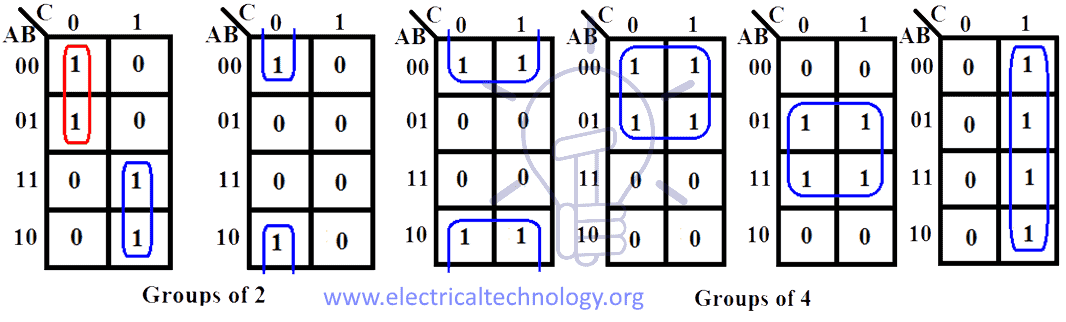
4. Group adjacent "1" cells: Identify groups of adjacent "1" cells, including those that wrap around the edges of the map. These groups represent minterms that can be combined for simplification.
5. Write the simplified expression: Based on the identified groups, write down the simplified Boolean expression.

Simplifying Boolean Expressions: Unlocking Efficiency

The primary benefit of using Karnaugh maps lies in their ability to simplify complex Boolean expressions. By grouping adjacent "1" cells, you can identify common variables and combine them into a single term. This process reduces the number of terms in the expression, leading to a simpler and more efficient circuit implementation.

Here are some key principles for grouping "1" cells:

• Adjacency: Cells are considered adjacent if they share a common edge, even if they wrap around the edges of the map.
• Group size: Groups should be as large as possible, with the size of the group being a power of two (1, 2, 4, 8, etc.).
• Minimum number of groups: Aim to cover all the "1" cells with the minimum number of groups.

Beyond Simplification: Applications of Karnaugh Maps

While simplification is the most prominent application, Karnaugh maps offer a range of benefits in digital circuit design:

• Logical optimization: K-maps facilitate the identification of redundant terms and the elimination of unnecessary logic gates, resulting in a more efficient circuit.
• Circuit implementation: By simplifying the Boolean expressions, K-maps help designers choose the appropriate logic gates for implementing the circuit, minimizing the number of gates required.
• Fault detection: The visual representation of the Boolean function allows for easier identification of potential faults in the circuit.
• Design analysis: K-maps provide a clear and concise representation of the circuit’s logic, facilitating analysis and understanding of the circuit’s behavior.

FAQ: Addressing Common Queries

Q1: Can Karnaugh maps be used for more than three variables?

A: Yes, Karnaugh maps can be extended to handle more than three variables, but the complexity of the map increases significantly. For four variables, a 4×4 grid is used, and for five variables, a 4×8 grid. However, the visual representation and simplification process become more challenging for higher numbers of variables.

Q2: What are the limitations of Karnaugh maps?

A: While powerful, Karnaugh maps have limitations, particularly for functions with a large number of variables. The visual representation becomes cumbersome and difficult to manage, making it less effective for complex circuits.

Q3: Are there alternative methods for simplifying Boolean expressions?

A: Yes, alternative methods exist, such as the Quine-McCluskey method, which is more suitable for handling Boolean expressions with a larger number of variables. However, Karnaugh maps remain a valuable tool for simplifying expressions with up to four or five variables due to their visual and intuitive nature.

Tips for Effective Karnaugh Map Usage

• Start with a clear understanding of the Boolean function: Ensure you have a well-defined expression before attempting to map it onto the K-map.
• Use a systematic approach: Follow a consistent method for labeling the rows, columns, and assigning values to the cells.
• Practice grouping techniques: Familiarize yourself with the principles of grouping adjacent "1" cells to achieve optimal simplification.
• Verify the simplified expression: After simplification, verify the resulting expression against the original function to ensure accuracy.
• Consider alternative methods for complex functions: For functions with a large number of variables, explore other simplification techniques like the Quine-McCluskey method.

Conclusion: Simplifying Complexity, Enhancing Efficiency

Karnaugh maps are a valuable tool in the arsenal of digital circuit designers, offering a visual and intuitive method for simplifying Boolean expressions. They enable efficient circuit implementation, optimize logic, facilitate fault detection, and provide a clear understanding of the circuit’s behavior. While limitations exist for highly complex functions, Karnaugh maps remain a powerful technique for simplifying expressions with up to four or five variables, contributing significantly to the design of efficient and reliable digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Three Variables. We thank you for taking the time to read this article. See you in our next article!