Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Four Variables

Related Articles: Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Four Variables

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Four Variables. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Four Variables

The realm of digital circuits and logic design is built upon the foundation of Boolean algebra. This powerful mathematical framework allows us to represent and manipulate logical relationships using variables and operators like AND, OR, and NOT. While these concepts are fundamental, their application can become complex, particularly when dealing with circuits involving multiple input variables. This is where Karnaugh maps, often referred to as K-maps, emerge as an invaluable tool.

Understanding Karnaugh Maps: A Visual Approach to Logic Minimization

Karnaugh maps are graphical representations of Boolean functions, providing a visual method to simplify and minimize logical expressions. They offer a systematic approach to identifying and combining adjacent minterms (product terms) in a truth table, leading to a simplified Boolean expression that corresponds to the same logic function.

The Essence of the K-map:

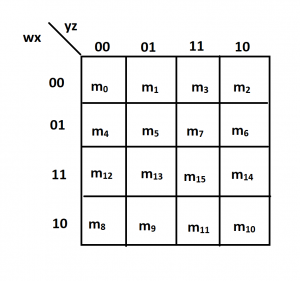
• Grid Representation: A K-map for a function with ‘n’ variables consists of a grid with 2^n cells, each cell representing a unique combination of input values.
• Binary Encoding: Each cell is labeled with a binary code corresponding to the input values it represents.
• Adjacent Cells: Cells that differ in only one bit position are considered adjacent. This concept is crucial for identifying and combining minterms.
• Grouping Minterms: The core principle of K-maps lies in grouping adjacent cells containing ‘1’s. These groups represent minterms that can be combined to simplify the Boolean expression.

Constructing a Karnaugh Map for Four Variables: A Step-by-Step Guide

Let’s delve into the process of constructing a K-map for a four-variable Boolean function. Consider the function F(A, B, C, D) = Σ(0, 2, 4, 6, 8, 10, 12, 14).

1. Define the Variables: Identify the four input variables: A, B, C, and D.
2. Create the Grid: Construct a 2^4 = 16-cell grid.
3. Label the Rows and Columns: Label the rows with the binary combinations of variables C and D, and the columns with the binary combinations of variables A and B. Note that the order of the labels is crucial to ensure adjacent cells differ by only one bit. This is achieved by using a Gray code sequence, where only one bit changes between consecutive labels.
4. Populate the Cells: For each minterm in the function’s sum-of-products form, place a ‘1’ in the corresponding cell of the K-map. For example, minterm 0 (A’B’C’D’) corresponds to cell (0,0), minterm 2 (A’B’CD’) corresponds to cell (0,1), and so on.

Visual Representation of the K-map:

	00	01	11	10
00	1	0	0	1
01	1	0	0	1
11	1	0	0	1
10	1	0	0	1

Simplifying Boolean Expressions Using K-maps: The Art of Grouping

The real power of K-maps lies in their ability to simplify Boolean expressions. This is achieved by identifying and combining adjacent groups of ‘1’s.

Rules for Grouping:

• Adjacent Cells: Groups must consist of adjacent cells, differing in only one bit position.
• Power of Two: Groups must contain a number of cells that is a power of two (1, 2, 4, 8, etc.).
• Largest Groups: Prioritize forming the largest possible groups to minimize the number of terms in the simplified expression.
• Wrap-Around: Cells on opposite edges of the K-map are considered adjacent.

Applying the Rules:

In the example K-map, we can form a single group encompassing all four ‘1’s in the first column. This group represents the minterm A’B’.

Simplified Expression:

The simplified Boolean expression for the given function is F(A, B, C, D) = A’B’.

The Benefits of Using Karnaugh Maps

Karnaugh maps offer significant advantages in logic design:

• Simplified Expressions: K-maps streamline the process of finding minimal Boolean expressions, reducing the complexity of circuits and lowering component count.
• Visual Clarity: The graphical representation of K-maps provides a clear and intuitive understanding of the relationships between input variables and output logic.
• Error Reduction: The visual nature of K-maps minimizes the risk of errors that can occur when manually manipulating complex Boolean expressions.
• Systematization: K-maps offer a systematic approach to logic minimization, ensuring consistency and reliability in design.

Frequently Asked Questions about Karnaugh Maps

Q1: Can Karnaugh maps be used for functions with more than four variables?

A: While K-maps are commonly used for up to four variables, their effectiveness diminishes with higher numbers of variables. For functions with five or more variables, alternative methods like Quine-McCluskey algorithm are more practical.

Q2: What if there are ‘don’t care’ conditions in the truth table?

A: ‘Don’t care’ conditions, denoted by ‘X’ in the K-map, represent input combinations that are irrelevant to the function’s output. They can be used to simplify the expression further by including them in groups of ‘1’s.

Q3: How do I handle functions with multiple outputs?

A: For functions with multiple outputs, you would create a separate K-map for each output, applying the same grouping and simplification techniques.

Tips for Effective Karnaugh Map Usage

• Start with the Truth Table: Construct the truth table for the function before creating the K-map.
• Use a Gray Code Sequence: Ensure the labels on the rows and columns follow a Gray code sequence to facilitate easy identification of adjacent cells.
• Prioritize Largest Groups: Focus on forming the largest possible groups to minimize the number of terms in the simplified expression.
• Don’t Forget Wrap-Around: Remember that cells on opposite edges of the K-map are considered adjacent.
• Check for Errors: Carefully review the grouped cells and the resulting simplified expression to ensure accuracy.

Conclusion: A Powerful Tool for Logic Design

Karnaugh maps are a valuable tool for simplifying Boolean expressions and minimizing logic circuits. They offer a visual and systematic approach to logic minimization, leading to more efficient and cost-effective designs. By understanding the principles of K-map construction and simplification, engineers and designers can effectively translate complex logical relationships into practical and optimized circuits. As we continue to advance in the realm of digital technology, Karnaugh maps will remain a cornerstone of logic design, ensuring the efficiency and reliability of the circuits that power our modern world.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Logic: A Comprehensive Guide to Karnaugh Maps for Four Variables. We appreciate your attention to our article. See you in our next article!