Demystifying Boolean Expressions: A Comprehensive Guide to Karnaugh Maps

Related Articles: Demystifying Boolean Expressions: A Comprehensive Guide to Karnaugh Maps

Introduction

With great pleasure, we will explore the intriguing topic related to Demystifying Boolean Expressions: A Comprehensive Guide to Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Expressions: A Comprehensive Guide to Karnaugh Maps

Boolean algebra, a fundamental concept in digital logic, provides a framework for representing and manipulating logical operations. It is the foundation for digital circuits, computer programming, and various other fields. One of the key tools for simplifying and optimizing Boolean expressions is the Karnaugh map, a visual representation that facilitates the identification of minimal expressions. This article delves into the intricacies of Boolean expressions, exploring their structure, applications, and the crucial role of Karnaugh maps in their simplification.

Understanding Boolean Expressions

Boolean expressions are logical statements composed of variables, operators, and constants. The variables represent propositions that can be either true (1) or false (0). The operators, such as AND (·), OR (+), and NOT (¬), define the logical relationships between these variables. Constants, typically represented by ‘0’ and ‘1’, represent fixed truth values.

Basic Boolean Operators:

• AND (·): The output is true only if all inputs are true.
  • Example: A · B is true only if both A and B are true.
• OR (+): The output is true if at least one input is true.
  • Example: A + B is true if either A or B or both are true.
• NOT (¬): The output is the opposite of the input.
  • Example: ¬A is true if A is false, and vice versa.

Example of a Boolean Expression:

F(A, B, C) = (¬A · B) + (A · ¬C)

This expression represents a function F that depends on variables A, B, and C. It states that F is true if either (¬A AND B) or (A AND ¬C) is true.

The Power of Karnaugh Maps

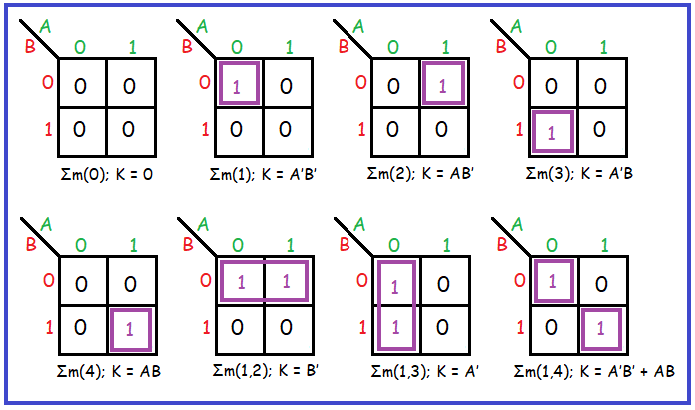
Karnaugh maps, also known as K-maps, provide a graphical method for simplifying Boolean expressions. They are particularly useful for expressions with up to four variables, offering a visual representation of the truth table and enabling the identification of minimal expressions.

Constructing a Karnaugh Map:

1. Determine the number of variables: The number of variables dictates the size of the K-map. For example, a three-variable function requires a 2×4 K-map, while a four-variable function needs a 4×4 K-map.

2. Assign binary values to each cell: Each cell in the K-map represents a unique combination of input values. These combinations are represented by binary numbers, with adjacent cells differing by only one bit.

3. Populate the map with output values: The output values for each input combination are entered into the corresponding cell. These values are typically ‘1’ for true and ‘0’ for false.

Simplifying Boolean Expressions using K-maps:

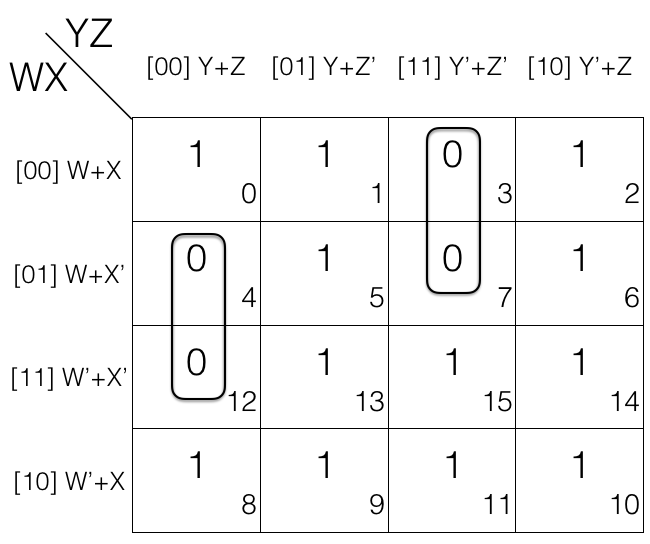
The key to simplifying expressions using K-maps lies in identifying groups of adjacent cells containing ‘1’ values. These groups, known as prime implicants, represent simplified terms in the Boolean expression. The goal is to find the minimal set of prime implicants that cover all ‘1’ cells in the map.

Rules for Grouping Cells:

• Adjacent cells: Groups can be formed by combining horizontally or vertically adjacent cells, including those that wrap around the edges of the map.
• Powers of two: The number of cells in a group must be a power of two (1, 2, 4, 8, etc.).
• Largest groups first: Prioritize grouping larger sets of ‘1’ cells to minimize the number of terms in the final expression.

Example:

Let’s consider a three-variable Boolean function:

F(A, B, C) = (A · ¬B) + (¬A · B) + (A · B · C)

The corresponding K-map is shown below:

	00	01	11	10
0	0	1	1	0
1	0	0	1	0

By grouping the ‘1’ cells, we can identify two prime implicants:

• Group 1: Cells (01, 11) representing (¬A · B) + (A · B) = B
• Group 2: Cell (11) representing (A · B · C)

The simplified expression for F is:

F(A, B, C) = B + (A · B · C)

Benefits of Using Karnaugh Maps

Karnaugh maps offer numerous advantages in simplifying Boolean expressions:

• Visual representation: The graphical nature of K-maps makes it easier to identify patterns and relationships between variables.
• Systematic approach: The process of grouping cells provides a structured and systematic way to simplify expressions.
• Minimal expressions: K-maps ensure that the simplified expression contains the minimum number of terms and literals.
• Easy to understand: Compared to algebraic manipulation, K-maps are relatively straightforward to understand and apply.
• Suitable for small-scale circuits: They are particularly effective for simplifying expressions with a limited number of variables.

Applications of Boolean Expressions and K-maps

Boolean expressions and Karnaugh maps find widespread applications in various domains:

• Digital circuit design: Simplifying Boolean expressions is crucial for designing efficient and cost-effective digital circuits.
• Computer programming: Logical operations are fundamental to programming languages, and K-maps can be used to optimize code efficiency.
• Artificial intelligence: Boolean expressions play a role in representing and manipulating knowledge in AI systems.
• Data analysis: Boolean logic is used in data mining and analysis to filter and extract information.
• Control systems: Boolean expressions are used to implement logic controllers in industrial automation and robotics.

FAQs about Boolean Expressions and K-maps

Q: What are the limitations of Karnaugh maps?

A: Karnaugh maps are primarily suitable for simplifying expressions with up to four variables. Beyond that, the visual representation becomes complex and difficult to manage.

Q: Can K-maps be used for expressions with more than four variables?

A: For expressions with more than four variables, other methods like the Quine-McCluskey algorithm or Boolean algebra manipulation are more practical.

Q: What are the alternative methods for simplifying Boolean expressions?

A: Besides K-maps, other methods include:

• Quine-McCluskey algorithm: This is a more systematic and algorithmic approach that can handle expressions with any number of variables.
• Boolean algebra manipulation: Using the laws and theorems of Boolean algebra, expressions can be simplified through algebraic manipulation.
• Computer-aided tools: Software programs specifically designed for logic simplification can handle complex expressions efficiently.

Q: How do I choose the most appropriate method for simplifying a Boolean expression?

A: The choice depends on factors like the number of variables, the complexity of the expression, and the desired level of accuracy. For small-scale expressions, K-maps are often sufficient. For larger expressions or those requiring higher accuracy, algorithmic methods or computer-aided tools are recommended.

Tips for Using Karnaugh Maps Effectively

• Start with a clear understanding of the Boolean expression: Ensure that you have correctly identified the variables, operators, and constants.
• Label the cells correctly: Make sure the binary values assigned to each cell are accurate and consistent.
• Group the ‘1’ cells systematically: Follow the rules for grouping cells, prioritizing larger groups and ensuring that all ‘1’ cells are covered.
• Double-check the simplified expression: Verify that the final expression is equivalent to the original expression and that it is indeed minimal.
• Practice with examples: Familiarize yourself with the process by working through numerous examples.

Conclusion

Boolean expressions form the backbone of digital logic, enabling the representation and manipulation of logical operations. Karnaugh maps provide a powerful visual tool for simplifying these expressions, offering a structured and efficient approach to identify minimal expressions. While K-maps are particularly effective for expressions with up to four variables, they serve as a valuable foundation for understanding the principles of Boolean simplification. By mastering the use of Karnaugh maps, one can gain valuable insights into the world of digital logic and its applications in various fields.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Expressions: A Comprehensive Guide to Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!