Demystifying Boolean Algebra: A Comprehensive Guide to Karnaugh Maps with Two Variables

Related Articles: Demystifying Boolean Algebra: A Comprehensive Guide to Karnaugh Maps with Two Variables

Introduction

With great pleasure, we will explore the intriguing topic related to Demystifying Boolean Algebra: A Comprehensive Guide to Karnaugh Maps with Two Variables. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Boolean Algebra: A Comprehensive Guide to Karnaugh Maps with Two Variables

The realm of digital logic, built upon the foundation of Boolean algebra, often presents a complex landscape for beginners. Understanding how to manipulate and simplify Boolean expressions is crucial for designing efficient digital circuits. While traditional algebraic methods can be cumbersome, Karnaugh maps (K-maps) offer a visually intuitive and powerful tool for simplifying Boolean expressions, particularly for functions with a small number of variables. This article delves into the intricacies of K-maps with two variables, providing a comprehensive understanding of their application and benefits.

Understanding the Basics: Boolean Expressions and Logic Gates

Before venturing into the realm of K-maps, it’s essential to grasp the fundamentals of Boolean algebra. Boolean algebra operates on binary values, represented by ‘0’ (false) and ‘1’ (true). These values are manipulated using logical operators such as:

• AND (· or ∧): Outputs ‘1’ only if both inputs are ‘1’.
• OR (+ or ∨): Outputs ‘1’ if at least one input is ‘1’.
• NOT (¬ or ¯): Inverts the input, changing ‘1’ to ‘0’ and vice versa.

These logical operators are implemented in digital circuits using logic gates. Each gate corresponds to a specific Boolean operator:

• AND gate: Outputs ‘1’ only when all inputs are ‘1’.
• OR gate: Outputs ‘1’ if at least one input is ‘1’.
• NOT gate (inverter): Inverts the input signal.

Introducing Karnaugh Maps: A Visual Approach to Boolean Simplification

Karnaugh maps provide a graphical representation of Boolean expressions, enabling efficient simplification by visually identifying and grouping terms. A K-map for two variables consists of a 2×2 grid, where each cell represents a unique combination of the two input variables. The rows and columns of the grid are labeled with the binary values of the input variables, ensuring that adjacent cells differ in only one variable.

Constructing a K-map:

1. Identify the input variables: Determine the variables influencing the Boolean function. For a two-variable K-map, these would be represented as ‘A’ and ‘B’.
2. Create the grid: Construct a 2×2 grid with rows and columns labeled with the binary values of the input variables. The top row represents ‘A’, and the leftmost column represents ‘B’.
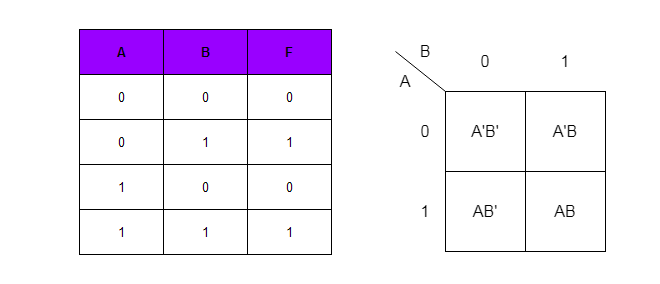
3. Populate the cells: Each cell in the grid corresponds to a unique combination of input values. For example, the top-left cell represents ‘A=0, B=0’, the top-right cell represents ‘A=0, B=1’, and so on.
4. Enter the function values: Assign ‘1’ to cells where the Boolean function evaluates to ‘1’, and ‘0’ to cells where it evaluates to ‘0’.

Simplifying Boolean Expressions using K-maps:

The beauty of K-maps lies in their ability to simplify Boolean expressions by visually identifying and grouping adjacent cells containing ‘1’s. These groups represent terms that can be combined using Boolean algebra rules.

Key rules for grouping terms:

• Adjacent cells: Groups must consist of cells that are adjacent to each other, either horizontally or vertically.
• Power of two: Groups must contain a number of cells that is a power of two (1, 2, 4, 8, etc.).
• Largest groups: Prioritize forming the largest possible groups to achieve the most simplified expression.
• Don’t care conditions: If the function’s value is unspecified for certain input combinations (represented by ‘X’ in the K-map), these cells can be included in groups to further simplify the expression.

Deriving the simplified expression:

Once the groups are identified, the simplified Boolean expression is derived by:

• Identifying the variables that are constant within each group: For example, if a group consists of cells where ‘A’ is always ‘1’ and ‘B’ varies, the term for that group would be ‘A’.
• Combining the terms for all groups using OR operation: Each group contributes a term to the final expression, which are combined using OR operation.

Illustrative Example: Simplifying a Two-Variable Boolean Expression

Consider the following Boolean expression:

F(A, B) = A'B + AB' + AB

Step 1: Construct the K-map:

AB	0	1
0	0	1
1	1	1

Step 2: Identify the groups:

• Group 1: Cells (0,1) and (1,1) form a group of two cells, where ‘B’ is always ‘1’.
• Group 2: Cells (1,0) and (1,1) form a group of two cells, where ‘A’ is always ‘1’.

Step 3: Derive the simplified expression:

• Group 1: The term for this group is ‘B’.
• Group 2: The term for this group is ‘A’.

Simplified expression:

F(A, B) = B + A

Benefits of Using Karnaugh Maps

K-maps offer numerous advantages over traditional algebraic methods for simplifying Boolean expressions:

• Visual intuition: The graphical representation allows for immediate identification of terms that can be combined.
• Efficiency: Simplifying expressions using K-maps is often faster and less prone to errors compared to algebraic manipulation.
• Handling complex expressions: K-maps can be effectively used to simplify expressions with up to four variables.
• Don’t care conditions: K-maps provide a convenient way to handle don’t care conditions, further simplifying the expression.

Frequently Asked Questions (FAQs)

Q1: Can K-maps be used for more than two variables?

A: Yes, K-maps can be used for expressions with up to four variables. For more variables, other methods like Quine-McCluskey algorithm are recommended.

Q2: What happens if there are no adjacent cells containing ‘1’s?

A: If there are no adjacent cells containing ‘1’s, the expression cannot be simplified further using K-maps. In this case, the original expression remains the simplified form.

Q3: How do I handle don’t care conditions in a K-map?

A: Don’t care conditions are represented by ‘X’ in the K-map. These cells can be included in groups to further simplify the expression.

Q4: What are the limitations of using K-maps?

A: K-maps become less efficient for expressions with more than four variables. Additionally, they may not always provide the most optimal simplification, especially for complex expressions.

Tips for Using Karnaugh Maps Effectively

• Start with a clear understanding of the Boolean function: Define the input variables and the desired output for each input combination.
• Organize the K-map correctly: Ensure that adjacent cells differ in only one variable and that the rows and columns are labeled correctly.
• Identify the largest possible groups: Prioritize forming the largest groups to achieve the most simplified expression.
• Consider don’t care conditions: Utilize don’t care conditions strategically to further simplify the expression.
• Verify the simplified expression: Double-check that the simplified expression is equivalent to the original expression by testing with different input combinations.

Conclusion

Karnaugh maps provide a powerful and intuitive tool for simplifying Boolean expressions, especially for functions with two or four variables. Their visual nature allows for rapid identification of terms that can be combined, leading to more efficient and compact digital circuit designs. By understanding the principles of K-maps and applying them effectively, designers can navigate the complexities of Boolean algebra with ease, paving the way for optimized and efficient digital systems.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Boolean Algebra: A Comprehensive Guide to Karnaugh Maps with Two Variables. We thank you for taking the time to read this article. See you in our next article!