A Deep Dive into Weighted Mean Absolute Percentage Error (WMAPE)

Related Articles: A Deep Dive into Weighted Mean Absolute Percentage Error (WMAPE)

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to A Deep Dive into Weighted Mean Absolute Percentage Error (WMAPE). Let’s weave interesting information and offer fresh perspectives to the readers.

A Deep Dive into Weighted Mean Absolute Percentage Error (WMAPE)

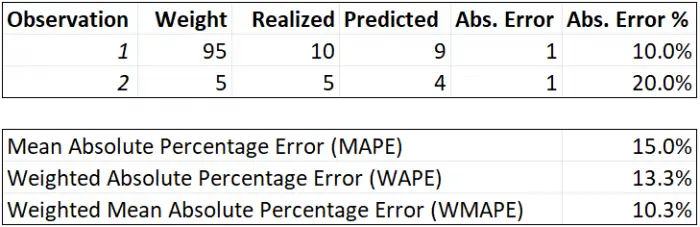
The realm of forecasting and performance evaluation is vast and intricate, demanding sophisticated tools to assess the accuracy of predictions. Among these tools, the Weighted Mean Absolute Percentage Error (WMAPE) stands out as a powerful metric for evaluating forecasting models, particularly when dealing with datasets exhibiting varying importance or scale across data points. This article delves into the intricacies of WMAPE, outlining its calculation, applications, strengths, and limitations, providing a comprehensive understanding of its role in the world of data analysis.

Understanding the Essence of WMAPE

WMAPE, a variation of the well-known Mean Absolute Percentage Error (MAPE), is a statistical measure that quantifies the average percentage error between forecasted and actual values. Unlike MAPE, which treats all data points equally, WMAPE assigns weights to each data point, reflecting their relative importance in the overall assessment. This weighting mechanism allows for a more nuanced and accurate evaluation of forecasting models, especially in scenarios where certain data points hold greater significance than others.

The Mathematical Foundation of WMAPE

The calculation of WMAPE involves a weighted average of the absolute percentage errors for each data point. The formula for WMAPE is:

*WMAPE = (∑ Wi |(Yi – Fi) / Yi|) / ∑ Wi**

Where:

• Wi: Weight assigned to the ith data point.
• Yi: Actual value of the ith data point.
• Fi: Forecasted value of the ith data point.

The weights (Wi) can be determined based on various factors, such as the volume of sales for a particular product, the importance of a specific customer, or the impact of a particular event on the overall forecast.

Applications of WMAPE: A Versatile Tool

WMAPE finds its applications in diverse fields, including:

• Financial Forecasting: In finance, WMAPE can be used to evaluate the accuracy of stock price predictions, where different stocks might have varying market capitalizations and hence different weights.
• Sales Forecasting: For businesses, WMAPE can assess the performance of sales forecasts for different products, considering factors like sales volume and profit margin.
• Supply Chain Management: In supply chain optimization, WMAPE can be used to evaluate the accuracy of demand forecasts for different products, taking into account the impact of stockouts and overstocking.
• Weather Forecasting: Meteorological agencies can utilize WMAPE to assess the accuracy of weather forecasts, weighting different regions based on population density or potential impact of weather events.

Advantages of WMAPE: A Refined Approach

WMAPE offers distinct advantages over traditional MAPE, making it a preferred choice in many scenarios:

• Account for Data Point Importance: By incorporating weights, WMAPE ensures that more significant data points have a greater influence on the overall error calculation.
• Reduced Bias: WMAPE mitigates the bias towards data points with smaller actual values that can occur with MAPE, especially when dealing with datasets containing outliers.
• Improved Accuracy: The weighting mechanism in WMAPE leads to a more accurate and representative evaluation of forecasting models, particularly when dealing with diverse and complex datasets.
• Greater Flexibility: WMAPE allows for customization by assigning weights based on specific criteria, making it adaptable to diverse forecasting challenges.

Limitations of WMAPE: Considerations and Caveats

While WMAPE offers significant advantages, it also has limitations that require careful consideration:

• Determining Weights: Assigning weights to data points can be subjective and requires careful consideration of the specific context and objectives of the analysis.
• Sensitivity to Outliers: Although WMAPE mitigates the impact of outliers to some extent, it can still be sensitive to extreme values, especially if they are assigned high weights.
• Computational Complexity: Calculating WMAPE can be computationally more demanding than MAPE, especially for large datasets with complex weighting schemes.

WMAPE: A Powerful Tool in the Data Analyst’s Arsenal

Despite its limitations, WMAPE remains a valuable tool for evaluating forecasting models, especially in scenarios where data points have varying importance. Its ability to incorporate weights and provide a more nuanced assessment of forecast accuracy makes it a powerful instrument for decision-making in diverse fields.

FAQs about WMAPE: Addressing Common Questions

1. What is the difference between WMAPE and MAPE?

While both WMAPE and MAPE measure the average percentage error, WMAPE incorporates weights for each data point, reflecting their relative importance, whereas MAPE treats all data points equally.

2. How do I choose appropriate weights for WMAPE?

The choice of weights depends on the specific context and objectives of the analysis. Consider factors like volume, impact, and significance of data points when assigning weights.

3. Can WMAPE be used for time series data?

Yes, WMAPE can be used for time series data, where weights can be assigned based on the time period or the importance of specific data points within the time series.

4. What are the limitations of using WMAPE?

WMAPE’s limitations include subjectivity in weight assignment, sensitivity to outliers, and computational complexity, especially for large datasets.

5. Is WMAPE always better than MAPE?

WMAPE is generally preferred when data points have varying importance, but it’s not always a superior metric. MAPE might be more suitable for datasets where all data points hold equal significance.

Tips for Using WMAPE Effectively: Maximizing its Utility

• Define Weights Carefully: Carefully consider the factors driving the importance of data points when assigning weights.
• Address Outliers: Implement appropriate outlier detection and handling techniques to minimize the impact of extreme values.
• Test Different Weighting Schemes: Explore different weighting schemes to find the most suitable approach for the specific context.
• Compare with Other Metrics: Evaluate the performance of forecasting models using WMAPE in conjunction with other metrics like MAPE and RMSE for a comprehensive assessment.

Conclusion: WMAPE – A Key Metric for Accurate Forecasting

WMAPE, with its ability to incorporate weights and provide a more nuanced evaluation of forecasting models, stands as a valuable tool for data analysts and decision-makers. Understanding its intricacies, advantages, and limitations is crucial for effectively utilizing this metric in diverse fields, ultimately leading to more accurate and informed predictions. By carefully considering the context and objectives of the analysis and applying appropriate weighting schemes, WMAPE can play a significant role in enhancing the accuracy and effectiveness of forecasting models, contributing to improved decision-making and enhanced outcomes.

Closure

Thus, we hope this article has provided valuable insights into A Deep Dive into Weighted Mean Absolute Percentage Error (WMAPE). We hope you find this article informative and beneficial. See you in our next article!